С появлением окружности, а затем колеса человечество сильно упростило себе жизнь.
И через много веков на ЕГЭ появились задачи по этой теме, конечно же
Зная свойства вписанного и центрального угла окружности, ты сможешь решить множество таких задач. И в этой статье мы тебе с этим поможем.
- Как измерить дуги и окружности
- Свойства вписанного угла и следствия из них
- Как выразить углы между хордами и секущими через центральный угол
- и многое другое…
Вписанный и центральный угол окружности — коротко о главном
Центр окружности – такая точка, расстояния от которой до всех точек окружности одинаковые.
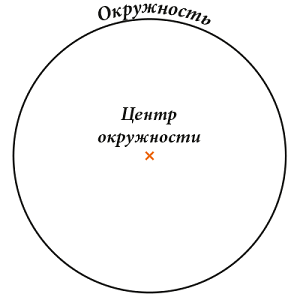
Радиус – отрезок, соединяющий центр и точку на окружности.
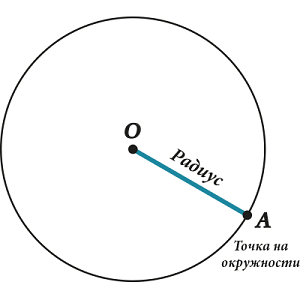
Радиусов очень много (столько же, сколько и точек на окружности), но длина у всех радиусов – одинаковая.
Что такое радиан? Чему он равен? И откуда он вообще взялся?
Иногда для краткости радиусом называют именно длину отрезка «центр – точка на окружности», а не сам отрезок.
А вот что получится, если соединить две точки на окружности? Тоже отрезок? Так вот, этот отрезок называется «хорда».
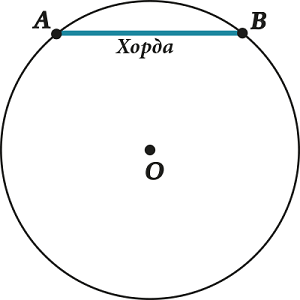
Тут есть ещё одно принятое выражение: «хорда стягивает дугу». Вот, здесь на рисунке, например, хорда ( displaystyle AB) стягивает дугу ( displaystyle AB).
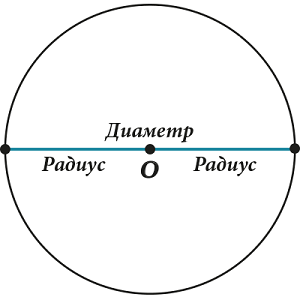
А если хорда вдруг проходит через центр, то у неё есть специальное название: «диаметр».
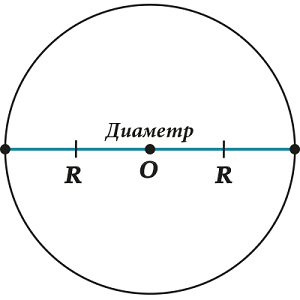
Так же, как и в случае с радиусом, диаметром часто называют длину отрезка, соединяющего две точки на окружности и проходящего через центр. Кстати, а как связаны диаметр и радиус? Посмотри внимательно. Конечно же,
Радиус равен половине диаметра.
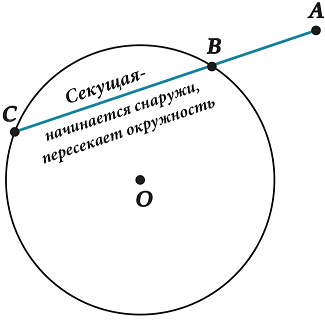
Кроме хорд бывают еще и секущие.
Вспомнили самое простое?
А теперь – названия для углов.
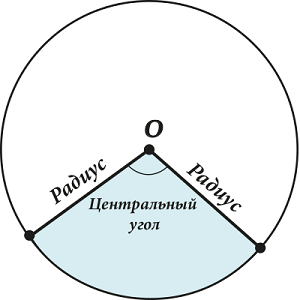
Центральный угол – угол между двумя радиусами.
Естественно, не правда ли? Стороны угла выходят из центра – значит, угол – центральный.
А теперь – вписанный угол.
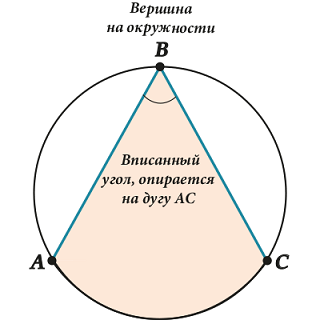
Вписанный угол – угол между двумя хордами, которые пересекаются в точке на окружности.
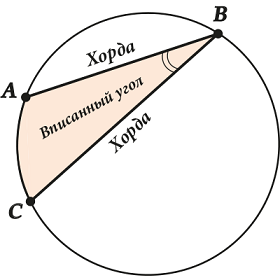
При этом говорят, что вписанный угол ( displaystyle ABC) опирается на дугу (или на хорду) ( displaystyle AC).
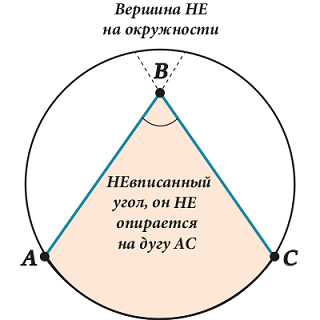
Вот здесь иногда возникают сложности. Обрати внимание – НЕ ЛЮБОЙ угол внутри окружности – вписанный, а только такой, у которого вершина «сидит» на самой окружности.
Что такое радиан?
Смотри на картинку:
Измерение дуг и углов окружности
Длина окружности. Дуги и углы измеряются в градусах и радианах.
Сперва о градусах
Для углов проблем нет – нужно научиться измерять дугу в градусах.
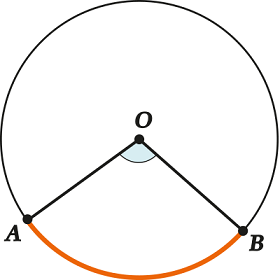
Градусная мера (величина дуги) – это величина (в градусах) соответствующего центрального угла
Что здесь значит слово «соответствующего»? Смотрим внимательно:
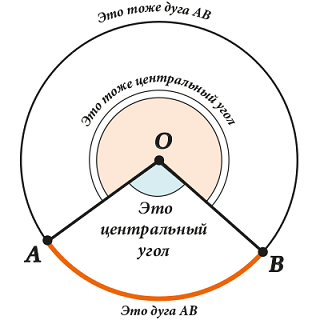
Видишь две дуги ( displaystyle AB) и два центральных угла?
Ну вот, большей дуге соответствует больший угол (и ничего страшного, что он больше ( displaystyle 180<>^circ )), а меньшей дуге соответствует меньший угол.
Итак, договорились: в дуге содержится столько же градусов, сколько в соответствующем центральном угле.
А теперь о радианах
Что же это за зверь такой «радиан»?
Представь себе: радианы – это способ измерения угла … в радиусах!
Угол величиной ( displaystyle 1) радиан – такой центральный угол, длина дуги которого равна радиусу окружности.
Тогда возникает вопрос – а сколько же радиан в развёрнутом угле?
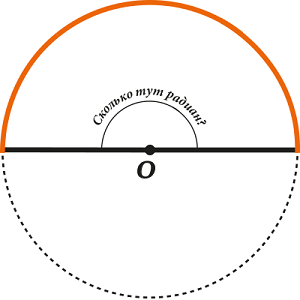
Иными словами: сколько радиусов «помещается» в половине окружности? Или ещё по-другому: во сколько раз длина половины окружности больше радиуса?
Этим вопросом задавались учёные ещё в Древней Греции.
И вот, после долгих поисков они обнаружили, что отношение длины окружности к радиусу никак не хочет выражаться «человеческими» числами вроде ( displaystyle 1,text< >2,text< >3,frac,frac) и т.п.
И даже не получается выразить это отношение через корни. То есть, оказывается, нельзя сказать, что половина окружности в ( displaystyle 2,5) раза или в ( displaystyle sqrt) раз больше радиуса!
Представляешь, как удивительно это было обнаружить людям впервые?! Для отношения длины половины окружности к радиусу на хватило «нормальных» чисел. Пришлось вводить букву ( displaystyle pi ).
Итак, ( displaystyle pi ) – это число, выражающее отношение длины полуокружности к радиусу.
Теперь мы можем ответить на вопрос: сколько радиан в развёрнутом угле? В нём ( displaystyle pi ) радиан. Именно оттого, что половина окружности в ( displaystyle pi ) раз больше радиуса.
Древние (и не очень) люди на протяжении веков (!) попытались поточнее подсчитать это загадочное число ( displaystyle pi ), получше выразить его (хоть приблизительно) через «обыкновенные» числа. А мы сейчас до невозможности ленивы – нам достаточно двух знаков после занятой, мы привыкли, что
( displaystyle pi approx 3,14)
Задумайся, это значит, например, что y окружности с радиусом единица длина приблизительно равна ( displaystyle 6,28), а точно эту длину просто невозможно записать «человеческим» числом – нужна буква ( displaystyle pi ).
И тогда эта длина окружности окажется равной ( displaystyle 2pi ). И конечно, длина окружности радиуса ( displaystyle R) равна ( displaystyle 2pi R).
Вернёмся к радианам.
Как перевести градусы в радианы: формулы перевода

С давних времён люди измеряют углы. Но что такое угол? Геометрия даёт нам ответ: «Угол — это два луча, проведённые из заданной точки». Углы бывают разные: тупые, острые, прямые, развёрнутые, центральные, смежные. Возьмём точку O и проведём из неё луч O. A. Теперь из этой же точки проведём луч OB, параллельный лучу OA и направленный с ним в одну сторону.
Про такие лучи говорят, что угол между ними составляет 0° (ноль градусов). Если мы теперь направим луч OB параллельно лучу OA, но в противоположную сторону, то получим развёрнутый угол, равный 180°.
Оглавление:
- Что означают градус и радиан
- Как перевести градусы в радианы и обратно
- Примеры решения задач
- Минуты и секунды
Что означают градус и радиан
Так вот, мерой расхождения двух лучей, проведённых из одной точки друг от друга, будет градусное расстояние. Что такое градус? В переводе «градус» означает «шаг». Всего таких «шагов» может быть 360°. Это число было придумано ещё в глубокой древности математиками и астрономами, пользовавшимися шестидесятиричной системой счисления.
Они брали круг, из центра которого проводили два радиуса. Мерой расхождения этих радиусов друг от друга был градус. Когда расстояние между радиусами в градусах отсчитывали против часовой стрелки, такой угол считался положительным, а когда против часовой — отрицательным.
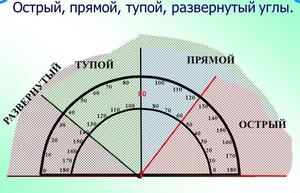
Вращая один радиус относительно другого против часовой стрелки, мы будем получать разные углы. Когда эти отрезки совпадают, то между ними будет 0°, когда же отрезки отсекают сектор круга, равный одной четверти полного круга, то угол между ними составит 90°. Вращая дальше таким образом, мы получим следующие углы: 180° — радиусы лежат на диаметре круга и делят его пополам, 270° — радиусы отсекают три четверти круга, 360° — радиусы совпадают. Таким образом, полный круг составляет 360°. Для измерения углов существует транспортир.
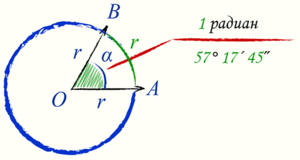
Кроме градусной меры для измерения углов применяют меру радианную. Радиан — это мера центрального угла. «Радиан» означает «связанный с радиусом». Если из центра окружности радиусом R провести два луча, то они на ней отсекут дугу, длина которой l. Так вот, угол α между указанными лучами называется центральным.
Чтобы его измерить, нужно длину дуги окружности разделить на её радиус: α=l/R. Получится значение, выраженное в радианах (рад). Поскольку любому углу на плоскости можно сопоставить такой же центральный угол, то встаёт вопрос, как от обычной градусной меры перейти к радианной.