S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.
Как найти площадь и периметр треугольника 3 класс?
P = a + b + c, где P — это периметр треугольника, a, b и c — его стороны.
Как вычислить площадь треугольника?
- Умножьте сторону треугольника на высоту, проведённую к этой стороне.
- Поделите результат на два.
Как найти площадь треугольника все формулы?
Площадь треугольника можно найти по формуле: S = 2R2 sin A sin B sin C , где A, B, С – углы треугольника, а R – радиус описанной окружности.
Как найти площадь прямоугольного треугольника зная катет и гипотенузу?
Поскольку катеты перпендикулярны, то один катет является высотой, проведенной к другому катету. Поэтому площадь прямоугольного треугольника равна половине произведения его катетов. площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе.
Площадь треугольника. Как найти площадь треугольника?
Как вычислить площадь треугольника из прямоугольника?
Определение : площадь прямоугольного треугольника равна произведению двух его катетов деленное на 2.
Что такое Что такое периметр треугольника?
Как узнать периметр треугольника
Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе. P = a + b + c, где a, b, c — длина стороны.
Как рассчитать площадь и периметр треугольника?
- Самая простая формула для расчета площади это произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2, .
- Вторая формула для расчета площади: по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p,
Что такое площадь 3 класс?
Площадь – внутренняя часть любой плоской геометрической фигуры. Квадрат – это прямоугольник, у которого все стороны равны. Прямоугольник – это четырёхугольник, у которого все углы прямые. Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Как найти площадь квадрата в 3 классе?
Площадь квадрата равна квадрату его стороны. Периметр квадрата равен сумме его четырех сторон.
Как найти площадь четырехугольника 3 класс?
‘Площадь = длина х высота, или S = a х h. Пример: если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь этого прямоугольника: S = 10 х 5 = 50 квадратных сантиметров.
Что нужно сделать чтобы найти площадь?
Когда известно значение длины и ширины фигуры
Для вычисления необходимо умножить их друг на друга. S = a * b, где S — площадь; a, b — длина и ширина.
Источник: topobzor10.ru
Площадь и периметр треугольника
Треугольник это геометрическая фигура (многоугольник), ограниченная со всех сторон замкнутой ломаной линией, состоящая из трех отрезков.
Формула периметра треугольника
Периметр треугольника равняется сумме всех его сторон: P = a + b + c,
где P это периметр и a, b, c – стороны треугольника.
Расчет периметра треугольника
Формула площади треугольника
1. Самая простая формула для расчета площади это произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2,
где S это площадь, a – основание, h – высота.
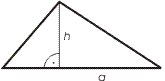
2. Вторая формула для расчета площади треугольника: по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p,
где r это радиус вписанной окружности, P – периметр треугольника, p – половина периметра треугольника (p = P/2)
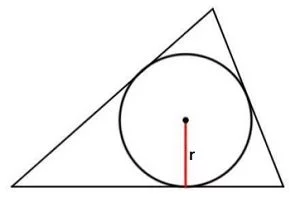
Расчет:
3. Площадь треугольника по двум сторонам и углу между ними: S = a · b · sin γ)/2 = (b · c · sin α)/2 = (a · c · sin β)/2,
где a, b, c это стороны треугольника и α, β, γ – его внутренние углы.
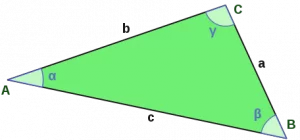
4. Формула Герона или площадь треугольника по его трем сторонам: S = √ p · (p — a)(p — b)(p — c) ,
где a, b и c это стороны треугольника и p – половина периметра треугольника.
Что такое периметр треугольника?
Периметром треугольника называется сумма длин всех его сторон.
Как найти/вычислить периметр треугольника?
Для получения периметра треугольника нужно сложить все его стороны: P = a + b + c,
где P это периметр и a, b, c – стороны треугольника.
Чему равен периметр треугольника?
Периметр треугольника равен сумме всех его сторон.
Как найти/посчитать площадь треугольника?
Для того, чтобы вычислить площадь треугольника, можно использовать одну из формул ее вычисления, используя доступные вводные данные.
- произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2,
где S это площдаь, a – основание, h – высота. - по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p,
где r это радиус вписанной окружности, P – периметр треугольника, p – половина периметра треугольника (p = P/2) - по двум сторонам и углу между ними: S = a · b · sin γ)/2 = (b · c · sin α)/2 = (a · c · sin β)/2,
где a, b, c это стороны треугольника и α, β, γ – его внутренние углы. - по трем сторонам: S = √ p · (p — a)(p — b)(p — c),
где a, b и c это стороны треугольника и p – половина периметра треугольника.
Целью Teadmiseks.ee является предоставление посетителям полезных инструментов в виде калькуляторов для различных расчетов и простых информационных страниц с данными, которые отвечают на определенные вопросы.
- Политика конфиденциальности
- Реклама
- Контакт
Red Hornet OÜ
Kungla põik 3-1, Peetri alevik, Rae vald
Площадь треугольника
Одну из сторон треугольника часто называют основанием. Если основание выбрано, то под словом «высота» подразумевают высоту треугольника, проведенную к основанию.
Теорема
| Площадь треугольника равна половине произведения его основания на высоту |
Доказательство
Дано: АВС, СН — высота, S — площадь АВС
Доказать: S = 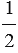 АВ
АВ  СН
СН
Доказательство:
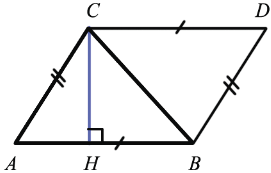
Достроим данный треугольник до параллелограмма ABCD так, как показано на рисунке.  АВС =
АВС =  DCB (по трем сторонам (ВС — общая, AB = CD и АС = BD как противоположные стороны параллелограмма ABCD)), а у равных многоугольников равные площади, значит площади данных треугольников равны. Следовательно, площадь S — площадь
DCB (по трем сторонам (ВС — общая, AB = CD и АС = BD как противоположные стороны параллелограмма ABCD)), а у равных многоугольников равные площади, значит площади данных треугольников равны. Следовательно, площадь S — площадь  АВС равна половине площади параллелограмма ABCD, т.е. S =
АВС равна половине площади параллелограмма ABCD, т.е. S = 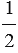 АВ
АВ  СН. Теорема доказана.
СН. Теорема доказана.
Следствие 1
| Площадь прямоугольного треугольника равна половине произведения его катетов |
Следствие 2
| Если высоты двух треугольников равны, то их площади относятся как основания |
Теорема
| Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы |
Доказательство
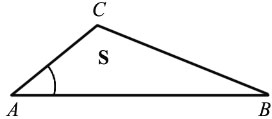
Дано:  АВС, СН — высота, S — площадь
АВС, СН — высота, S — площадь  АВС,
АВС,  А1В1С1, В1Н1 — высота, S1 — площадь
А1В1С1, В1Н1 — высота, S1 — площадь  А1В1С1,
А1В1С1, 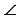 А =
А = 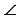 А1
А1
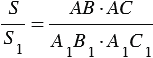
Доказать:
Доказательство:
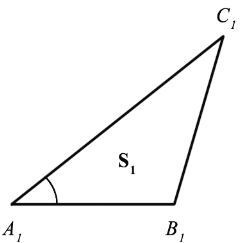
Наложим треугольник А1В1С1 на треугольник АВС так, чтобы вершина А1 совместилась с вершиной А, а стороны А1В1 и А1С1 наложились соответственно на лучи АВ и АС.
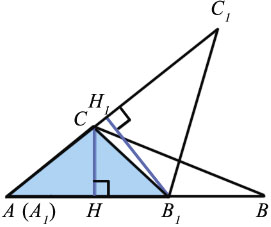
Треугольники АВС и АВ1С имеют общую высоту СН, поэтому
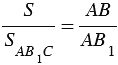
Треугольники АВ1С и АВ1С1 также имеют общую высоту — В1Н1, поэтому
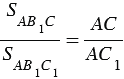
Перемножая полученные равенства, находим:
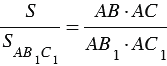 или
или 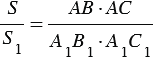
Теорема доказана.
Источник: budu5.com