ОГЭ по математике 2024, все задания ФИПИ с ответами
Какие задания будут на ОГЭ по математике в этом году? Только задания из открытого банка ФИПИ. Как самостоятельно подготовиться к экзамену, если не работает открытый банк заданий ФИПИ? Просто зайти на ГДЗответ ру! У нас для вас задания с ФИПИ с ответами к ОГЭ по математике в 9 классе. Любые из этих вариантов могут вам попасться на реальном ОГЭ в этом году.
Если у вас возник вопрос, какие задания будут в этом году на ОГЭ по математике, добро пожаловать на ГДЗответ ру. Мы собрали только те задания, которые вам встретятся на реальном экзамене, и подготовили ответы к ним. Задания классифицированы по линейкам с номером вопроса, теория в отдельных статьях, есть ответы ко всем заданиям ФИПИ. Есть шпоры к каждому заданию. Никаких Ященко!
Гущин со своими пособиями тоже «отдыхает»! Будем готовиться на высший балл непосредственно по вопросам, которые будут на реальном ОГЭ в этом году. После прочтения и запоминания всего, что есть в этом разделе, вы сможете с уверенностью сказать: «Я решу ОГЭ по математике на максимальный балл!»
Алгебра. Как найти значение выражения?
- Вы здесь:
- ОГЭ по математике 2024, все задания ФИПИ с ответами
Источник: gdzotvet.ru
Математика 6 класс «Буквенные выражения»


Презентация для проведения урока математики в 6 классе. Вводит учащихся в тему Буквенные выражения, содержит определение буквенного выражения, и разбор заданий на нахождение значения буквенного выражения, при заданном значении переменной. Рекомендованное домашнее задание можно найти на сайте УЧИ.РУ, математика 6 класс, Буквенные выражения.
мат6 Буквенные выражения.pptx
Классная работа Буквенные выражения

23.12 Классная работа Буквенные выражения
Буквенные выражения – это выражение составленное из чисел, переменных и знаков действий.
Значение выражения получается, если переменной придать значение

Значение выражения получается, если переменной придать значение
Пример: найти значение выражения
Найти значение выражения

Найти значение выражения
Найти значение выражения
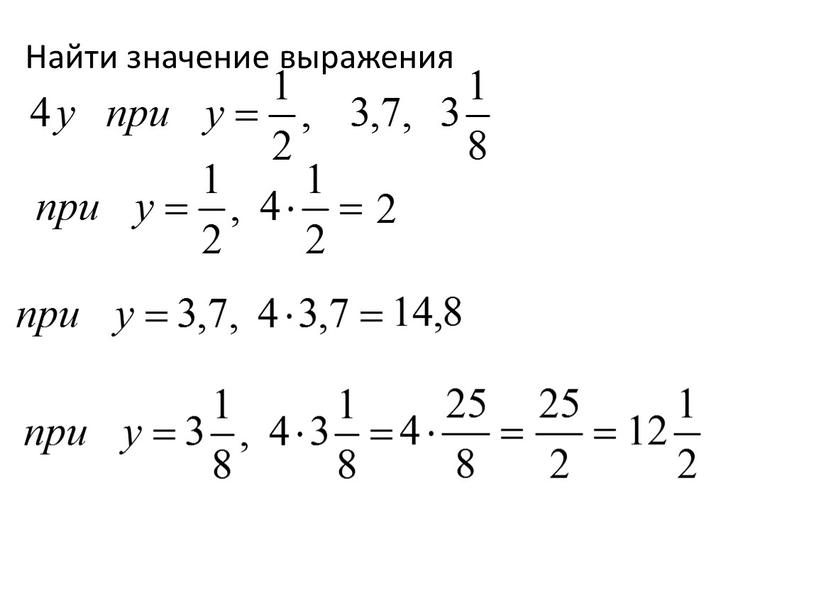
ОГЭ по математике. Задание 1. Найти значение выражения
Найти значение выражения
Найти значение выражения Домашнее задание:

Найти значение выражения
Домашнее задание: УЧИ.РУ №264 22.12 — 26.12
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Источник: znanio.ru
Решение производной для чайников: определение, как найти, примеры решений

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента.
Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте.
Пример. Вычислим производную:

Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:


Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:


Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:


