Как решать дроби Ютуб

Калькулятор дробей выполнит основные арифметические действия с дробями и смешанными числами.

Если целая часть заполнена, калькулятор приведет смешанное число в неправильную дробь и выполнит операцию.

Заполните поля калькулятора чтобы найти сумму, разность, произведение и отношение дробей.

Основные операции с дробями

Сложение и вычитание

Чтобы сложить дроби с разными знаменателями необходимо: привести дробные части к наименьшему общему знаменателю; затем сложить их числители. Рассмотрим на примере как сложить две дроби с разными знаменателями.

Пример Сложить дроб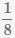и и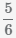

.

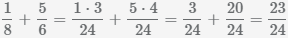
Наименьшее общее кратное знаменателей (8 и 6) равно 24.

Сложение дробей. Как складывать дроби?

Для нахождения разности дробей необходимо: привести дробные части к наименьшему общему знаменателю; затем выполнить вычитание числителей.

Пример Найти разность дробе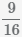й и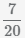

.

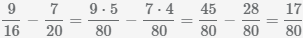
Общее кратное знаменателей НОК(16, 20)=80. Для вычисления наименьшего общего кратного можно воспользоваться калькулятором. Калькулятор вычислит НОК автоматически.

Умножение и деление

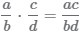
Для умножения двух дробей нужно: перемножить их числители и знаменатели .

Пример Найти произведение дробе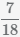й и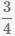

.

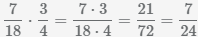
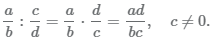
Чтобы разделить дробь на другую нужно: умножить первую дробь на дробь, обратную второй: .

Пример Разделить дробь на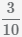

.

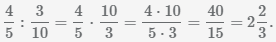
Приведение к общему знаменателю

Чтобы совершать операции с дробями часто требуется привести дроби к общему знаменателю. Рассмотрим процесс приведения двух дробе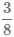й и 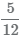к наименьшему общему знаменателю :

КАК НАУЧИТЬСЯ СЧИТАТЬ ДРОБИ / ВСЕГО 3 ПРАВИЛА

• 1 Находим наименьшее общее кратное знаменателей: НОК(8, 12)=24. Число 24 является наименьшим общим знаменателем двух дробей, приведем обе дроби к данному знаменателю. Любые две дроби можно привести к одинаковому знаменателю.
• 2 Вычисляем дополнительный множитель первой дроби 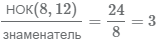. Умножаем числитель и знаменатель на дополнительный множитель 3, получаем дробь .
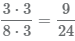• 3 Вычислим дополнительный множитель второй дроби 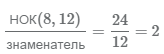. Умножаем числитель и знаменатель на дополнительный множитель 2, получаем дробь .
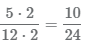• 4 В результате получим дроб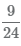и и 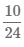с одинаковым знаменателем равным 24.

Пример Сравнить дроб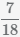и и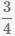

Для сравнения дробей приведем их к общему знаменателю и сравним их числители. Воспользуемся шагами описанными выше и найдем наименьшее общее кратное знаменателей дробей и далее преобразуем:

.

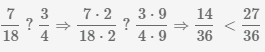
НОК(18, 4)=36, дополнительный множитель первой дроби 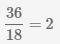, доп. множитель второй дроби .

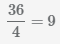Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Источник: calcs.su

Деление обыкновенных дробей: правила, примеры, решения

Из статьи вы узнаете, как поделить одну обыкновенную дробь на другую, обыкновенную дробь на натуральное число и натуральное число на обыкновенную дробь. Подробно расскажем о делении дробей и смешанных чисел.

Как проводить деление обыкновенных дробей

Правило деления обыкновенных дробей следующее:

1. Числитель первой из дробей следует помножить на знаменатель второй. Полученный результат будет числителем новой дроби;
2. Знаменатель первой из дробей следует помножить на числитель второй. Полученное число буде знаменателем новой дроби.

Для деления обыкновенных дробей следует первую из них умножить на дробь обратную второй.

Деление дробей с разными знаменателями проводится аналогичным образом. Какие у них знаменатели, значения не имеет.

Поделить (3/5) на (7/8).

(3/5) : (7/8) = (3/5)*(8/7) = 24/35

Ответ: 24/35.

Поделить (2/5) на (8/15).

(2/5) : (8/15) = (2/5) * (15/8) = (2*15)/(5*8).

Сокращаем на 5 и на 2.

В результате имеем (2/5) : (8/15) = ¾

Поделить (4/7) на (2/5).

(4/7) : (2/5) = (4/7) * (5/2) = 10/7

Полученная дробь неправильная, поэтому выделим из неё целое число. В результате получим 1(3/7).

Деление обыкновенных дробей на число

Как известно, любое натуральное число можно записать как дробь, у которой знаменатель равняется одному. Например, число 2 можно записать, как (2/1), а число 7 записать, как (7/1). При осуществлении деления обыкновенной дроби на натуральное число этим правилом очень активно пользуются.

Для деления дроби на натуральное число следует это самое число записать в виде дроби, а затем провести деление согласно правилам.

Пример: Поделить (5/9) на 2.

Решение:

Записываем 2 как 2/1. Получается

Ответ: 5/18.

Нет времени решать самому?

Наши эксперты помогут!

Нужна помощь

Деление натурального числа на обыкновенную дробь

Что бы поделить натуральное число на обыкновенную дробь нужно число умножить на дробь обратную данной.

Проще говоря, меняем у делителя числитель со знаменателем местами и умножаем результат на наше число.

Поделить 5 на (5/12).

Решение: Делаем смену числителя и знаменателя у (5/12) местами. Получаем (12/5). Далее имеем 5* (12/5) = (5*12)/5 = 12

Поделить 8 на (4/5).

Решение: Делаем смену числителя и знаменателя у (4/5) местами. Получаем (5/4). Далее имеем 8* (5/4) = (8*5)/4 = (2*5)/1 =10

Поделить 27 на (9/5).

Решение: Делаем смену числителя и знаменателя у (9/5) местами. Получаем (5/9). Далее имеем 27* (5/9) = (27*5)/9 = (3*5)/1 =15

Правило деления дробей на смешанные числа

При делении смешанных дробей и обыкновенных дробей смешанные дроби преобразуются в неправильные. После этого деление происходит по приведённым выше правилам.

Примеры ниже пояснят сказанное.

Поделить 3(3/4) на 75.

Переводим 3(3/4) в (3 * 4 + 3)/4 = 15/4.

Теперь нам нужно разделить 15/4 на 75. Это делается по ранее изложенным правилам деления обыкновенной дроби на число.

Сокращаем результат на 15. В результате имеем 3(3/4) : 75 = 1/(4*5) = 1/20

Поделить 40 на 8(3/10).

Переводим 8(3/10) в неправильную дробь (8*10 + 3)/4 = 83/4.

Далее 40 : (83/10) = 40 * (10/83) = 400/83. Сокращению она никак не поддаётся, но можно выделить целую часть. Это мы и делаем.

Ответ: 4(68/83).

Поделить 2(8/45) на 28/15.

Переводим 2(8/45) в неправильную дробь 2(8/45) = (2*45 – 8)/45 = 98/45.

Затем выполняем деление по уже известным нам правилам (98/45) : (28/15) = (98/45) * (15/28). Её можно сократить.

Для начала следует разложить числители и знаменатели на множители [(2*7*7)*(3*5)]/[(3*3*5)*(2*2*7)].

Сокращаем на 3, на 7 и на 2. В завершение будем иметь 7/(3*2) = 7/6.

Полученная дробь оказалась неправильной. Извлекаем из неё целую часть 7/6 = 1(1/6).

Деление дроби на смешанное число проводится аналогичным образом, с соблюдением всех указанных правил. Только будьте внимательны при выделении целой части и сокращении, когда проводите эти действия.

Источник: www.napishem.ru

Рациональные (обыкновенные) дроби и действия с ними. Простые числа

Подробнее

Подробнее

Подробнее

Готовиться с нами — ЛЕГКО!

Эффективное решение существует!

Вы ищете теорию и формулы для ЕГЭ по математике ? Образовательный проект «Школково» предлагает вам заглянуть в раздел «Теоретическая справка». Здесь представлено пособие по подготовке к ЕГЭ по математике, которое фактически является авторским. Оно разработано в соответствии с программой школьного курса и включает такие разделы, как арифметика, алгебра, начала анализа и геометрия (планиметрия и стереометрия). Каждое теоретическое положение, содержащееся в пособии по подготовке к ЕГЭ по математике, сопровождается методически подобранными задачами с подробными разъяснениями.

Таким образом, вы не только приобретете определенные знания. Полный справочник для ЕГЭ по математике поможет вам научиться логически и нестандартно мыслить , выполнять самые разнообразные задачи и грамотно объяснять свои решения. А это уже половина успеха при сдаче единого государственного экзамена.

После того, как вы нашли необходимые формулы и теорию для ЕГЭ по математике, рекомендуем вам перейти в раздел «Каталоги» и закрепить полученные знания на практике. Для этого достаточно выбрать задачу по данной теме и решить ее. Кроме того, справочные материалы по математике для ЕГЭ пригодятся вам и для других естественнонаучных дисциплин, таких как физика, химия и т. д.

Факт 1.
(bullet) Множество натуральных чисел (mathbb) – это числа (1, 2, 3, 4 ) и т.д.
(bullet) Множество целых чисел (mathbb) состоит из натуральных чисел, противоположных им ( (-1, -2, -3 ) и т.д.) и нуля (0) .
(bullet) Рациональные числа (mathbb) – числа вида (dfrac ab) , где (ain mathbb) , (bin mathbb) (обыкновенные дроби). Таким образом, существует включение: (mathbb) содержится в (mathbb) , а (mathbb) содержится в (mathbb) .
Это просто термины, которые стоит запомнить, чтобы правильно понимать условия задач.

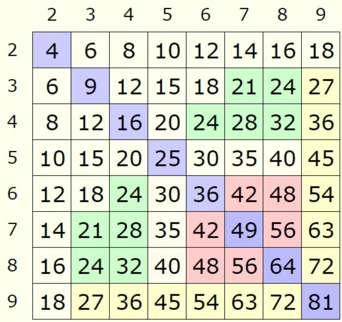
Факт 2.
Таблица умножения:
Заметим, что любое целое число можно представить в виде дроби. Например, (3=dfrac31) .
Также напоминаем, что при умножении на любое число (не равное нулю) числителя и знаменателя дроби значение этой дроби не меняется. Например, (dfrac31=dfrac62=dfrac93) и т.п.

Факт 3.
(bullet) Простое число – это натуральное число, имеющее ровно два делителя: (1) и само это число.
Пример: (2, 3, 5, 7, 11, 13, 17) и т.д.
Заметим, что число (1) не является простым, так как делится только на (1) , то есть имеет ровно один делитель.
(bullet) Признак делимости на (2) : число (a) делится на (2) , если оно заканчивается на (0,2,4,6) и (8) . Например, числа (56) и ( 900) делятся на (2) , а числа (71) и ( 1973) не делятся на (2) . Числа, делящиеся на (2) , называются четными; числа, не делящиеся на (2) , называют нечетными.
Признак делимости на (3) : число (a) делится на (3) , если его сумма цифр делится на (3) . Например, числа (198) и ( 105) делятся на (3) , а числа (179) и ( 5869) не делятся на (3) .
Признак делимости на (5) : число (a) делится на (5) , если оно заканчивается на (5) или на (0) . Например, числа (505) и ( 160) делятся на (5) , а число (367) не делится на (5) .
Признак делимости на (9) : число (a) делится на (9) , если его сумма цифр делится на (9) . Например, числа (198) и ( 108) делятся на (9) , а числа (149) и ( 5109) не делятся на (9) .
Признак делимости на (10) : число (a) делится на (10) , если оно заканчивается на (0) . Например, числа (50) и ( 160) делятся на (10) , а число (367) не делится на (10) .
(bullet) Разложение числа на простые множители – это запись этого числа в виде произведения простых чисел.
Пример: (4200=2^3cdot 3cdot 5^2cdot 7) .
Как разложить число на простые множители? Покажем на примере. Пусть нужно разложить число (4200) на простые множители. Видим, что число (4200) делится на (100) , причем (4200:100=42) . Следовательно, (4200=100cdot 42) . Так как (100=10cdot 10=2cdot 5cdot 2cdot 5=2^2cdot 5^2) , а (42=6cdot 7=2cdot 3cdot 7) , то получаем: [4200=2^2cdot 5^2cdot 2cdot 3cdot 7=2^3cdot 5^2cdot 3cdot 7] Разложение на простые множители используется при сокращении дробей. (bullet) Сокращение дробей – деление числителя и знаменателя на одно и то же число, отличное от нуля.
Пример: (begin >=dfrac3\[2ex] <7llapcdot 5>=dfrac 85\[2ex] 2llapcdot 2cdot 7>>=dfracend) Заметим, что если ответом к задаче является дробь, то она должна быть несократимой, то есть ее числитель и знаменатель не должны иметь общих делителей. Например, будет неправильным записать ответ к задаче как (dfrac) . Нужно заметить, что (65=13cdot 5) , следовательно, [dfrac=dfrac<13llap>>=dfrac15] То есть правильным ответом будет (dfrac15) .

Факт 4.
(bullet) Правила сложения дробей: Значит, когда мы складываем две дроби с одинаковыми знаменателями, мы получаем дробь, у которой :
– знаменатель остается таким же;
– числитель равен сумме числителей этих двух дробей.
Точно так же мы поступаем и с разностью двух дробей. Значит, когда мы складываем две дроби с разными знаменателями, мы:
– приводим их к одинаковому знаменателю, домножив первую дробь на знаменатель второй, а вторую – на знаменатель первой;
– таким образом мы получаем две дроби с одинаковыми знаменателями и их можно сложить как дроби с одинаковыми знаменателями (то есть пользуясь первой формулой).
Это первый, более сложный способ сложения двух дробей с разными знаменателями. Второй способ, который упрощает вычисления и тем самым уменьшает вероятность допустить вычислительную ошибку, будет показан чуть позже
Примеры: 1) (dfrac 6+dfrac 6=dfrac6=dfrac6) 2) (dfrac2-dfrac2=dfrac2=dfrac62) 3) (dfrac12+dfrac3=dfrac=dfrac) (bullet) Правила умножения дробей: Если мы умножаем две дроби, то мы получаем дробь, у которой:
– числитель равен произведению числителей двух дробей;
– знаменатель равен произведению знаменателей двух дробей. Пример: (dfrac 47cdot dfrac5=dfrac) (bullet) Правила деления дробей: Данное правило часто называют так: >. Пример: 1) (dfrac 45 :dfrac 67=dfrac 45cdot dfrac 76) ; 2) (dfrac 12_3=dfrac12:dfrac31=dfrac12cdot dfrac13=dfrac16) (bullet) Для того, чтобы перевести дробь смешанную дробь, например, (4dfrac) , в неправильную, нужно проделать следующие действия: [4+dfrac5=dfrac41+dfrac5=dfrac=dfrac]
(bullet) Разложение чисел на простые множители, помимо сокращения дробей, необходимо для того, чтобы наиболее оптимально приводить дроби к общему знаменателю (общий знаменатель – число, которое делится на знаменатель каждой дроби).
Пусть нам нужно привести две дроби (dfrac1) и (dfrac1) к общему знаменателю. По правилу из Факта 3 можно просто перемножить их знаменатели и получить дроби (dfrac) и (dfrac) . Но тогда общий знаменатель этих дробей получается достаточно большим: (15cdot 21=315) . Покажем другой оптимальный способ приведения дробей к общему знаменателю.

Так как (21=7cdot 3) и (15=3cdot 5) , то наименьшее число, которое делится и на (21) , и на (15) – это (7cdot 3cdot 5=105) . Следовательно, это и есть их наименьший общий знаменатель. Для того, чтобы дробь (dfrac1) имела знаменатель (105) , нужно умножить ее числитель и знаменатель на (5) ; для того, чтобы дробь (dfrac1) имела знаменатель (105) , нужно умножить ее числитель и знаменатель на (7) . Таким образом, получаем: (dfrac1=dfrac5) и (dfrac1=dfrac7) . Покажем еще один пример, демонстрирующий, что не всегда удобно и нужно раскладывать знаменатели прямо до простых множителей. Пусть нам нужно сложить дроби (dfrac1) и (dfrac1) . Замечаем,что (98=2cdot 49) (для того, чтобы это заметить, нужно хорошо выучить таблицу умножения и потренировать устный счет ). Тогда можно записать (dfrac1) и (dfrac1) . Следовательно, для того, чтобы у дробей стали одинаковые знаменатели, нужно всего лишь домножить первую дробь на (2) : (dfrac2) и (dfrac1) . А теперь представьте, что вы пользуетесь первым способом. Тогда ваш общий знаменатель будет равен (49cdot 98=4802) ! Неудобно, верно?

Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.

Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?

1. Потому что это расширяет кругозор . Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.
2. Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.

Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.

Источник: shkolkovo.net