Как решать систему уравнений Ютуб

Напомним для начала определение решения системы уравнений с двумя переменными.

Определение 1

Пара чисел называется решением системы уравнений с двумя переменными, если при их подстановки в уравнение получается верное равенство.

В дальнейшем будем рассматривать системы из двух уравнений с двумя переменными.

Существуют четыре основных способа решения систем уравнений: способ подстановки, способ сложения, графический способ, способ ведения новых переменных. Рассмотрим эти способы на конкретных примерах. Для описания принципа использования первых трех способов будем рассматривать систему двух линейных уравнений с двумя неизвестными:

Способ подстановки

Способ подстановки заключается в следующем: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$

[left< begin \ end right.]

Выразим из второго уравнения $y$ через $x$:

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | Математика

Подставим в первое уравнение, найдем $x$:

Ответ: $(-2, 3)$

Способ сложения.

Рассмотрим данный способ на примере:

[left< begin \ end right.]

Умножим второе уравнение на 3, получим:

Теперь сложим оба уравнения между собой:

Найдем $y$ из второго уравнения:

Ответ: $(-2, 3)$

Замечание 1

. Отметим, что в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении одна из переменных «исчезла».

«Системы уравнений с двумя переменными, способы решения»
Готовые курсовые работы и рефераты
Решение учебных вопросов в 2 клика
Помощь в написании учебной работы

Графический способ

Графический способ заключается в следующем: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.

[left< begin \ end right.]

Выразим из обоих уравнений $y$ через $x$:

Изобразим оба графика на одной плоскости:

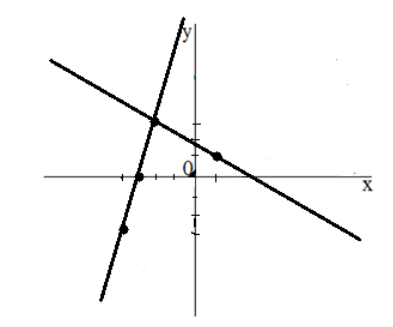
Ответ: $(-2, 3)$

Способ введения новых переменных

Этот способ рассмотрим на следующем примере:

[left< begin -3^y=-1> \ end right.]

Решение.

Данная система равносильна системе

Пусть $2^x=u (u>0)$, а $3^y=v (v>0)$, получим:

Решим полученную систему методом сложения. Сложим уравнения:

Тогда из второго уравнения, получим, что

Возвращаясь к замене, получим новую систему показательных уравнений:

Ответ: ($0,1$).

Источник: spravochnick.ru

Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными

Разность двух чисел равна 4, а их произведение 12. Найдите эти числа.

Решение систем уравнений методом подстановки

Решение:

Обозначим первое число буквой , а второе буквой . По условию задачи разность чисел равна 4, т.е. — = 4.

Так как произведение чисел равно 12, то = 12.

Системы уравнений, решению систем линейных уравнений

Определение: — такое значение переменной или такой упорядоченный набор значений зміниих, что удовлетворяет сразу всем уравнениям системы, то есть розвязком системы двух или более уравнений с неизвестными называется такое упорядоченное множество множество чисел, при подстановке которых в систему вместо неизвестных все уравнения превращаются в верные числовые равенства.

Определение: — найти все ее развязки или доказать, что их нет.

Если система не имеет решения, то она несовместима.

Примеры систем

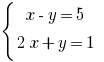
— система двух уравнений с двумя переменными

Пара 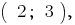то есть 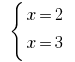—решение системы

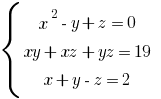
— система трех уравнений с тремя переменными

Тройка 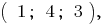то есть 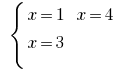— один из розвязків системы

Схема решению систем уравнений

Графический метод

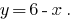
1. Выполняем равносильные преобразования, так, чтобы было удобно построить график функции. Например:
2. Строим графики.
3. Находим точки пересечения графиков. Координаты этих точек и есть розвязком данной системы уравнений.

Метод подстановки

1. Из одного уравнения системы выражаем одну переменную через другую, всегда выбираем удобную переменную. Например, из уравнения 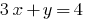выражаем переменную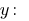 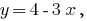а не наоборот.
2. Найденное значение подставляем в другое уравнение системы и получаем уравнение с одной переменной.
3. Розвязуємо полученное уравнение
4. Найденное значение подставляем в выраженное уравнение, и находим значение второй переменной.

Метод сложения

1. Урівнюємо коэффициенты при одной из переменных путем по членного умножения обоих уравнений на множители, подобранные соответствующим образом.
2. Добавляем (или отнимаем) почленно два уравнения системы, тем самым исключается одна переменная.
3. Розвязуємо полученное уравнение.
4. Подставляем найденное значение переменной в любое из исходных уравнений.

Примеры решению систем уравнений

Решению графическим методом

Пример 1

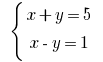
Розвяжіть уравнения:

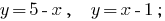
Строим графики

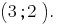
Построив графики увидим, что графики пересекаются в точке

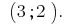
Ответ:

Решению методом подстановки

Пример 2

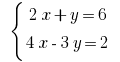
Розвяжіть уравнения:

Из первого уравнения выражаем 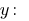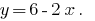А полученное выражение подставляем во второе уравнение системы:

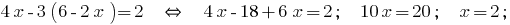
Полученное значение подставляем в выражение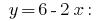

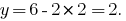
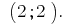
Ответ:

Решению методом добавления

Пример 3

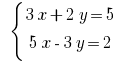
Розвяжіть уравнения:

Должны избавиться от переменной Умножаем почленно первое уравнение системы на 3, а второе – на 2.

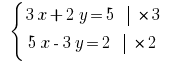
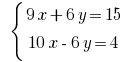
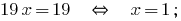
Добавляем почленно уравнение и получаем:

Находим значение из первого уравнения системы: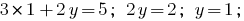

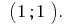
Ответ:

Замечание: В методе добавления можно умножать не только на положительные числа, а и на отрицательные.

Каким способом розвязувати систему уравнений решать только Вам.

Источник: cubens.com