Как решать уравнения с дробями Ютуб

Содержание

Дробное уравнение — уравнение вида — Решение дробных уравнений , то и — некоторые многочлены. Дробное уравнение равносильно системе:

Решение дробных уравнений

Решение дробного уравнения можно разбить на два этапа:

Решение дробных уравнений

1) решить уравнение ;

Решение дробных уравнений

2) проверить условие .

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Примеры с решением

Пример 1:

Решить дробное уравнение:

Решение дробных уравнений

Как решать уравнения с дробью? #shorts

а)

Решение:

Соберем дроби в левую часть уравнения и приведем их к общему знаменателю:

Решение дробных уравнений

Получившееся уравнение равносильно системе:

Решение дробных уравнений

Возможно вам будут полезны данные страницы:

Пример 2:

Решение дробных уравнений

Решим уравнение

Решение:

Решение дробных уравнений

Уравнение имеет два корня.

Решение дробных уравнений

Проверим корни на выполнение второго условия системы.

Если Решение дробных уравнений , то , следовательно, число является посторонним корнем данного уравнения.

Если Решение дробных уравнений , то , следовательно, число является корнем данного уравнения.

Решение дробных уравнений

Ответ: .

Пример 3:

Решение дробных уравнений

Решить уравнение с дробями — Математика — 6 класс

Решение:

Преобразуем левую и правую части уравнения:

Решение дробных уравнений

Полученное уравнение равносильно системе:

Решение дробных уравнений

Пример 4:

Решение дробных уравнений

Решим уравнение

Решение:

Решение дробных уравнений

Уравнение имеет два корня.

Решение дробных уравнений

Проверим корни на выполнение второго условия системы.

Если Решение дробных уравнений , то , следовательно, число является корнем данного уравнения.

Решение дробных уравнений

Ответ:

Пример 5:

Решение дробных уравнений

Решение:

Преобразуем числитель дроби, стоящей в левой части уравнения:

Решение дробных уравнений

Так как числитель дроби Решение дробных уравнений равен то дробь ни при каких допустимых значениях переменной не будет принимать значение, равное нулю. Следовательно, исходное уравнение не имеет решений.

Ответ: нет решений.

Пример 6:

Решение дробных уравнений

Решение:

Преобразуем выражение, стоящее в левой части уравнения:

Решение дробных уравнений

Корнем данного уравнения является любое действительное число, кроме .

Еще по теме: Ютуб узнай меня если сможешь все

Решение дробных уравнений

Ответ: любое действительное число, кроме .

Решение дробных уравнений

Собственные значения матрицы
Решение разных задач методом гаусса
Связь между графиком функции и графиком ее производной
Предел последовательности. Свойства сходящихся последовательностей
Задача двойной интеграл. Определение. Основные свойства двойного интеграла
Разложение на множители
Деление многочлена на многочлен
Правила дифференцирования
Теорема Пифагора
Производная экспоненты

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

В случае копирования материалов, указание web-ссылки на сайт natalibrilenova.ru обязательно.

Источник: natalibrilenova.ru

Дробные уравнения, как розвязати дробное уравнение

Использование уравнений-следствий

Сводим к виду
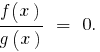
Находим корни уравнения
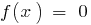
Выполняем проверку подстановкой в исходное уравнение

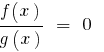
Использование свойств соответствующих функций

Фиксируем ОДЗ начального уравнения
Сводим к виду и розвязуємо эти уравнения на ОДЗ исходного или выполняем равносильные преобразования так, чтобы ввести удобную замену переменных.
Выполняем проверку подстановкой в исходное уравнение

Источник: cubens.com