Вопрос по математике:
Несколько приятелей при встрече пожали друг другу руки. Сколько встретилось приятелей, если рукопожатий было 10?
А. 5.
Б. 4. В. 3.
Г. 2.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
- bookmark_border
- 22.10.2015 17:35
- Математика
- remove_red_eye 19298
- thumb_up 10
Ответы и объяснения 1
wherschinede204
Допустим, встретилось всего 2 приятеля. Тогда было всего 1 рукопожатие.
Пусть теперь встретилось 3 приятеля. Теперь рукопожатий стало 3.
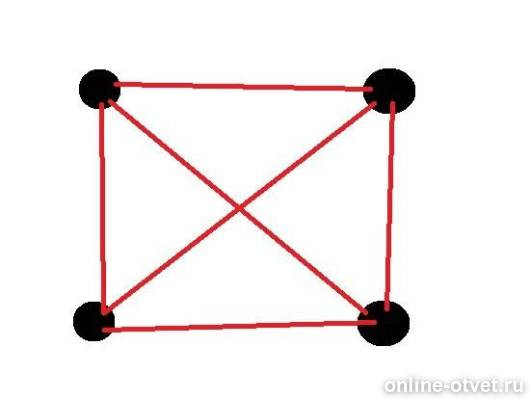
При встрече 4 приятелей стало 6 рукопожатий. (см. рисунок)
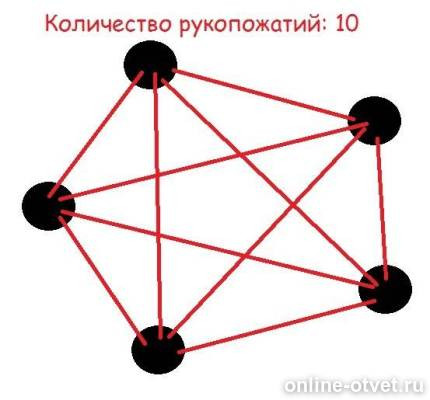
При встрече 5 приятелей стало 10 рукопожатий. (см. рисунок)
(количество рукопожатий определяется количеством красных линий)
КОГДА БАТЯ и МАМА ПОШЛИ НА ВЕЧЕР ВСТРЕЧИ ВЫПУСКНИКОВ
- 24.10.2015 00:15
- thumb_up 11
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
Источник: online-otvet.ru
На встрече выпускников бывшие одноклассники пожали друг другу руки всего было 231

July 2022 1 3 Report
30 бывших одноклассников пришли на встречу выпускников. Все 30 поздоровались друг с другом без исключения. Сколько было сделано рукопожатий?
Прим. Когда человек А жмет руку человеку В , человек В тоже жмет руку. Это считается одним рукопожатием.
Богатенький одноклассник смеялся, когда он мыл его машину, а на встрече выпускников…
Answers https://scholar.tips/30-byvshih-odnoklassnikov-prishli-na-vstrechu-vypusknikov-vse-30-pozdorovalis-dru.html» target=»_blank»]scholar.tips[/mask_link]
На встрече выпускников бывшие одноклассники пожали друг другу руки всего было 231
На встречу выпускников пришло 45 человек. Оказалось, что любые двое из них, имеющие одинаковое число знакомых среди пришедших, не знакомы друг с другом. Какое наибольшее число пар знакомых могло быть среди участвовавших во встрече?
Решение
Поскольку 45 = 1 + 2 + 3 + . + 9, можно разбить 45 человек на группы по 1, 2, . 9 человек. Пусть люди, принадлежащие одной группе, не знакомы между собой, а люди, принадлежащие разным группам, знакомы. Тогда каждый человек из k-й группы имеет 45 – k знакомых.
При этом условие задачи выполнено, и общее количество пар знакомых людей равно
Докажем, что большего числа знакомств быть не могло. Зафиксируем некоторое k, 0 ≤ k ≤ 44. Пусть некоторый выпускник знаком ровно с k другими. По условию никакой из его знакомых не может иметь ровно k знакомых. Поэтому количество выпускников, знакомых ровно с k другими, не превосходит
45 – k.
Обозначим через A0, A1, . A44 количество выпускников, имеющих соответственно 0, 1, . 44 знакомых. Как показано выше, Ak ≤ 45 – k, кроме того, A0 + A1 + . + A44 = 45.
Оценим общее число знакомств: 2S = A1 + 2A2 + . + 44A44 = A44 + (A44 + A43) + . + (A44 + A43 + . + A36) + . + (A44 + A43 + . + A0) ≤
≤ 1 + (1 + 2) + . + (1 + 2 + . + 9) + 45 + 45 + . + 45 = 1 + 3 + 6 + 10 + 15 + 21 + 28 + 36 + 36·45 = 1740.
Ответ
Источники и прецеденты использования
| олимпиада | |
| Название | Всероссийская олимпиада по математике |
| год | |
| Год | 2003 |
| Этап | |
| Вариант | 4 |
| Класс | |
| Класс | 10 |
| задача | |
| Номер | 03.4.10.3 |
Проект осуществляется при поддержке и .
Источник: problems.ru