В комплект входят векторные иконки (логотипы) социальных сетей: Вконтакте, Facebook, Instagram, Twitter, Pinterest; а также сервисов: Skype, Dropbox, YouTube, Telegram, Dribbble, WhatsApp и другие. Качественные иконки популярных социальных сетей, можно скачать одним файлом.
![]()
![]()
Скачать формат: ai и pfd
Быстрая и бесплатная загрузка:
Tags:
First Share
da.indsd
— ведем собственный электронный дневник, сохраняя в нем все самое интересное связанное с дизайном. Записываем не одну определенную тему, а несколько, таких как дизайн рекламы, промышленный дизайн, архитектурный дизайн и свободное творчество. Собираем полезный материал для работы.
Источник: da.indsd.com
Логотипы социальных сетей в векторе
Популярные значки социальных сетей и мессенджеров: ВКонтакте, Одноклассники, Мой мир, Viber, Telegram, Skype, Facebook, YouTube, WhatsApp, Instagram, LinkedIn, Twitter, Google+, Pinterest, Tumblr. Все логотипы доступны для скачивания бесплатно, во всех распространенных векторных форматах (EPS 10v, AI cs4, CDR 13v).
Одноклассник который все понимает буквально
Всего представлено 15 круглых лого соцсетей в едином стиле оформления. Иконки подойдут для размещения ссылок на профиль в макете, на сайте и т. д.

Все значки легко редактируются, масштабируются и перемещаются в нужной последовательности. Ниже можно просмотреть шаблон открытый в Adobe Illustrator:

Также макет выглядит и в CorelDraw.

Иконки популярных российских и зарубежных соцсетей вы можете скачать бесплатно, без рекламы по кнопке ниже.

После подтверждения e-mail файл будет доступен в личном кабинете. По всем вопросам пишите в форму обратной связи (левый нижний угол) указав свой e-mail.
(Visited 24 081 times, 5 visits today)
Посмотрите еще статьи по данной теме:
Голосуем за статью!
(6 оценок, среднее: 5,00 из 5)
Один комментарий к “Логотипы социальных сетей в векторе”
Как заказать макет штампа для высечки.
Есть ли у вас готовые решения макетов коробок для высечки.
Спасибо.
Источник: expert-polygraphy.com
Как выражать вектор? Как решать задачу с вектором? | TutorOnline
Вектор
Сегодня нас ждёт увлекательное путешествие, которое можно озаглавить словосочетанием «векторы в геометрии». Да, достаточно самонадеянно думать, что меньше чем за час можно стать экспертом в этой теме. Но познакомиться, выяснить нюансы, а главное, увидеть всю картину целиком — можно! Мы постараемся стать вашими проводниками в этот удивительный мир и охватить все темы о векторах, которые могут встретиться в школе.
20 сентября 2022
· Обновлено 15 мая 2023
Определение и обозначение вектора
Вектор в геометрии — это отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом. В некоторых учебниках вектор могут называть направленным отрезком.
Вектор обозначается одной строчной буквой латинского алфавита или двумя заглавными со стрелкой (в некоторых случаях — прямой линией) сверху.
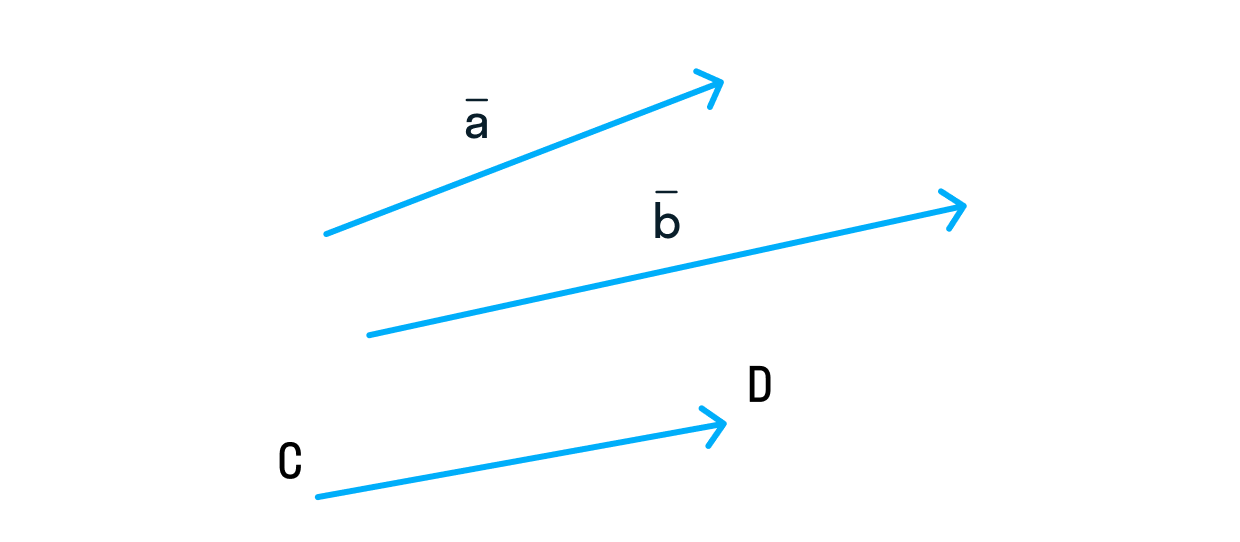
Интересно, что порядок букв в названии вектора имеет значение! Первая буква отвечает за начало вектора, а последняя — за его конец. Поэтому и — абсолютно разные векторы.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
![]()
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.

Виды векторов
Во-первых, векторы бывают коллинеарными и неколлинеарными.
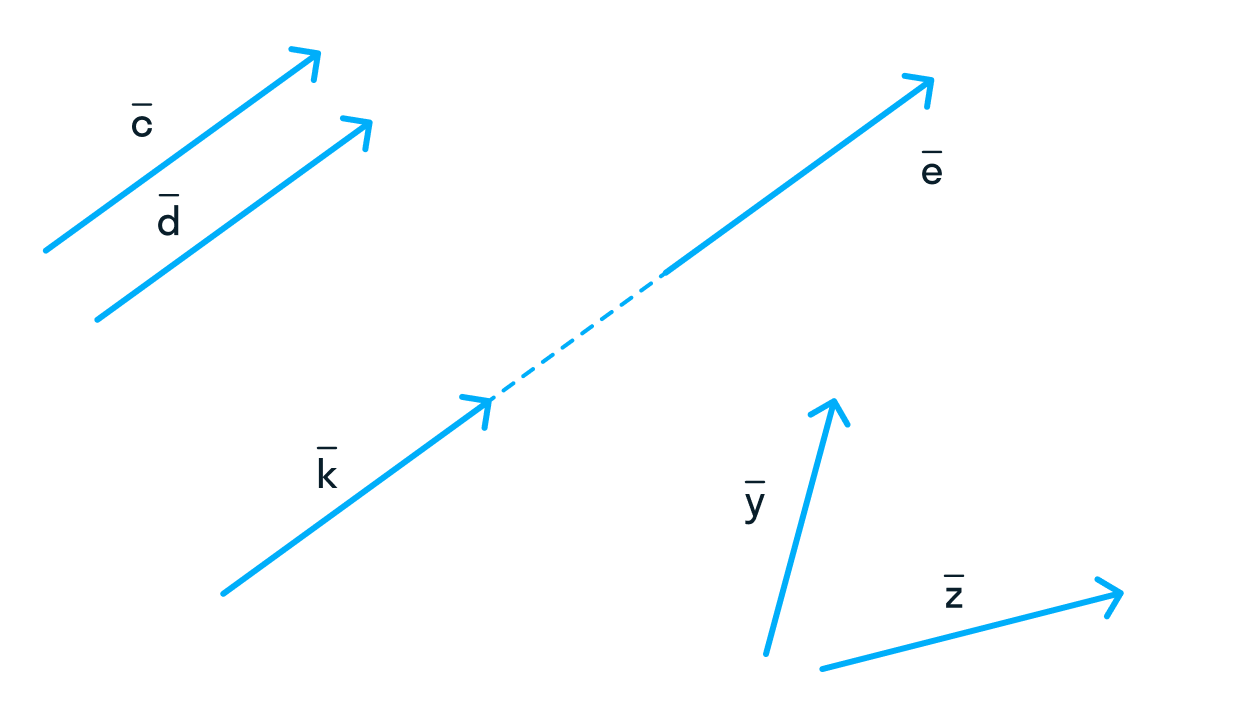
Коллинеарными называют те векторы, которые лежат на одной прямой или параллельных прямых. На рисунке и и являются коллинеарными, а и относительно друг друга — нет.
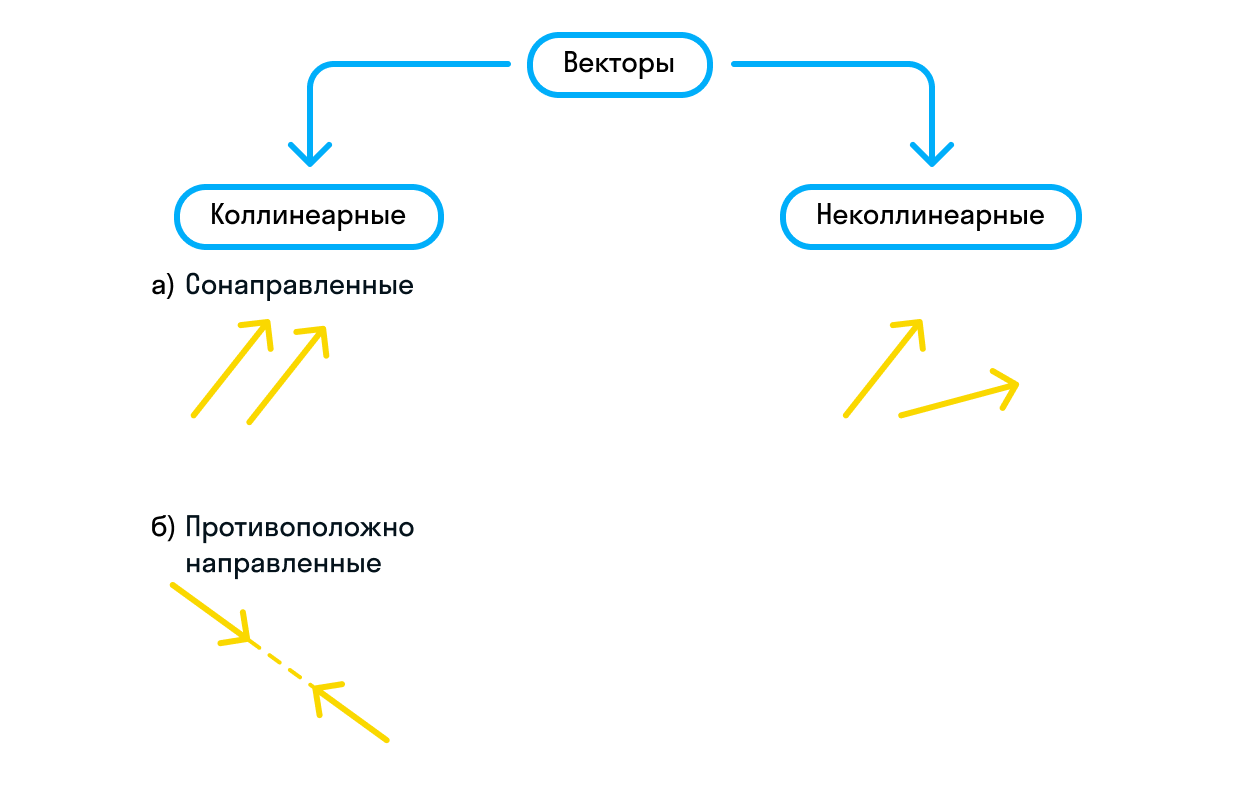
Векторы различаются и по направлению. Если векторы уже являются коллинеарными, они могут быть сонаправленными или противоположно направленными. Сонаправленные векторы обозначаются так: Если же они противоположно направлены, мы можем записать это следующим образом:
Равными являются те векторы, которые одновременно и коллинеарны, и сонаправлены, а также имеют одинаковую длину.
Нулевой вектор — вектор, длина которого равна нулю. Чаще всего его обозначают так: Он считается коллинеарным любому вектору.
Иногда в геометрии вводят дополнительные понятия, рассмотрим и их:
- Закреплённый вектор — отрезок с упорядоченными концами: если С — точка начала вектора, а Е — точка конца, тогда (это то, что мы понимаем под обычным вектором в школьной геометрии).
- Свободный вектор — вектор, начало и конец которого не закреплены. Его можно перемещать как вдоль прямой, на которой он находится, так и параллельно этой прямой. По сути под свободным вектором понимают множество закреплённых векторов.
Сложение и вычитание векторов
Действия с векторами описываются и в алгебре, и в геометрии. Сегодня мы рассмотрим способы, благодаря которым можно сложить и вычесть векторы, не зная их координат.
Сложение: метод треугольника
Представим, что в пространстве заданы векторы и которые нам необходимо сложить. Эта задача особенно актуальна для физиков, поскольку такие векторные величины, как сила, часто приложены к одному и тому же телу. В таком случае возникает вопрос: а как же рассчитать результирующее действие всех этих сил?
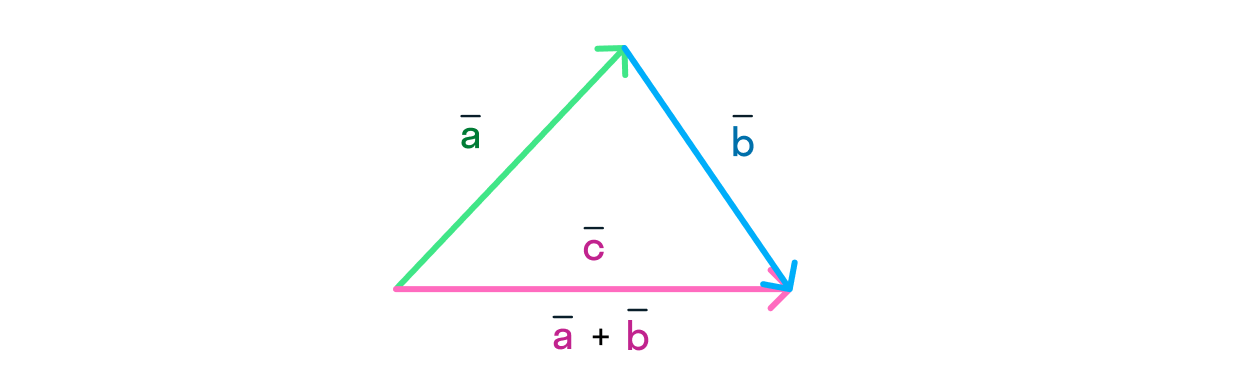
В этом на помощь физикам приходит математика — царица наук! Чтобы сложить два вектора, необходимо:
- Отложить начало одного вектора от конца другого.
- Вектор их суммы будет совпадать с вектором , который соединяет начало вектора с концом вектора
Сложение: метод параллелограмма
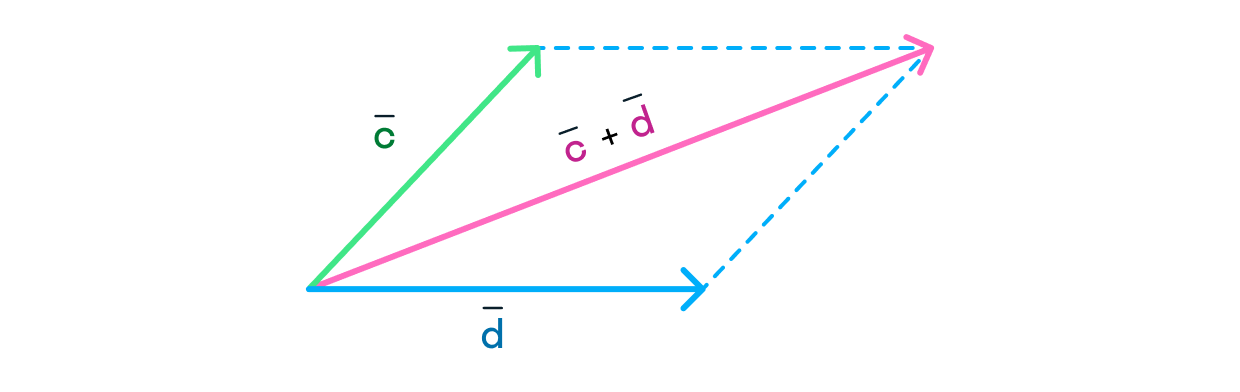
Сложить векторы можно и по-другому, используя метод параллелограмма:
- Совместим между собой начала и
- Отложим от конца вектор, равный
- Отложим от конца вектор, равный
- Благодаря пунктам 2 и 3 мы получили параллелограмм (четырёхугольник, противоположные стороны которого параллельны и равны).
- Проведём диагональ параллелограмма между и на которой будет лежать вектор, равный сумме и
Задача решена, вы великолепны!
Обратите внимание
Как метод параллелограмма, так и метод треугольника подразумевает перемещение векторов в пространстве: мы или совмещаем их начала, или откладываем от конца одного вектора начало другого. Получить сумму векторов, не имеющих общей точки, с этими методами не представляется возможным.
Сложение: метод многоугольника
А что если векторов больше, чем два? На эту проблему математика уже подготовила решение: воспользуемся расширенным методом треугольника, который получил название «метод многоугольника».
Согласно этому методу мы последовательно совмещаем конец и начало векторов, а после изображаем суммирующий вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего. Лучше всего рассмотреть это на чертеже:
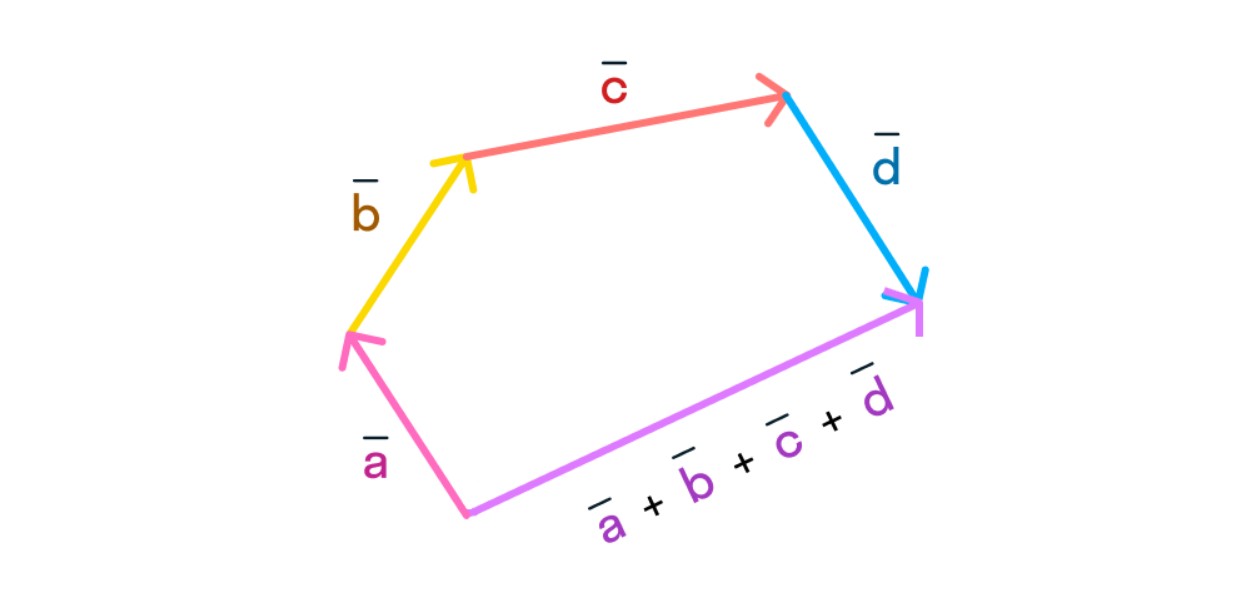
Вычитание векторов
Продолжаем проделывать с векторами всевозможные действия, на этот раз вычитание. Математики знают, что вычитание — это по своей сути то же сложение, но с обратным числом.
С векторами работает та же штука: вместо вычитания попробуем прибавить вектор, противоположно направленный исходному:
Изобразим разность векторов с помощью уже знакомого нам правила треугольника:
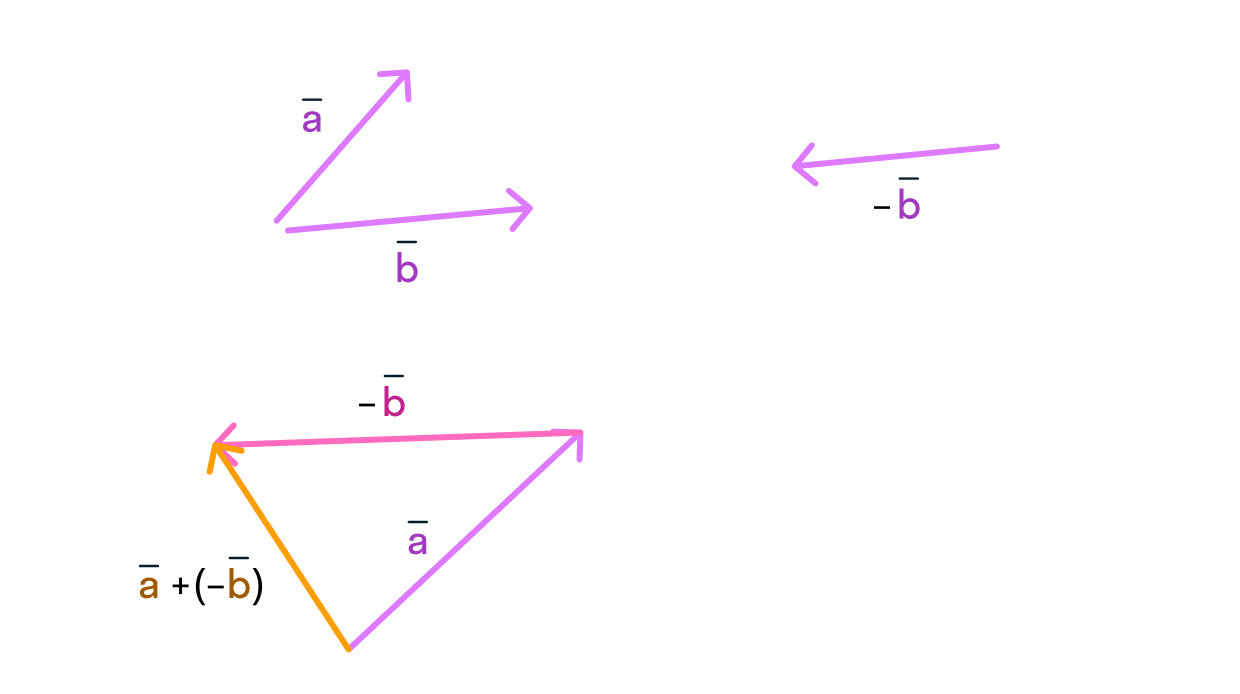
Боитесь запутаться в векторах сонаправленных и противоположно направленных? Существует отдельное правило для их вычитания:
- Отложим один вектор от начала другого.
- Тогда вектор их разности совпадает с вектором, начало которого совмещено с концом вычитаемого вектора, а конец — с концом уменьшаемого.

Этот метод схож и с методом параллелограмма, но в этом случае мы берём другую диагональ.
Координаты вектора на плоскости и в пространстве
Для выполнения остальных действий с векторами нам необходимо поместить их в такую систему координат, чтобы можно было определить их положение относительно друг друга. Для этого используют декартову систему координат, которой можно пользоваться как на плоскости с осями X и Y, так и в пространстве с осями X, Y, Z.
Тогда, если находится на плоскости, его координаты можно выразить как если в пространстве —
Базисные векторы — это векторы, каждый из которых направлен вдоль своей оси координат, в трёхмерном пространстве их обозначают
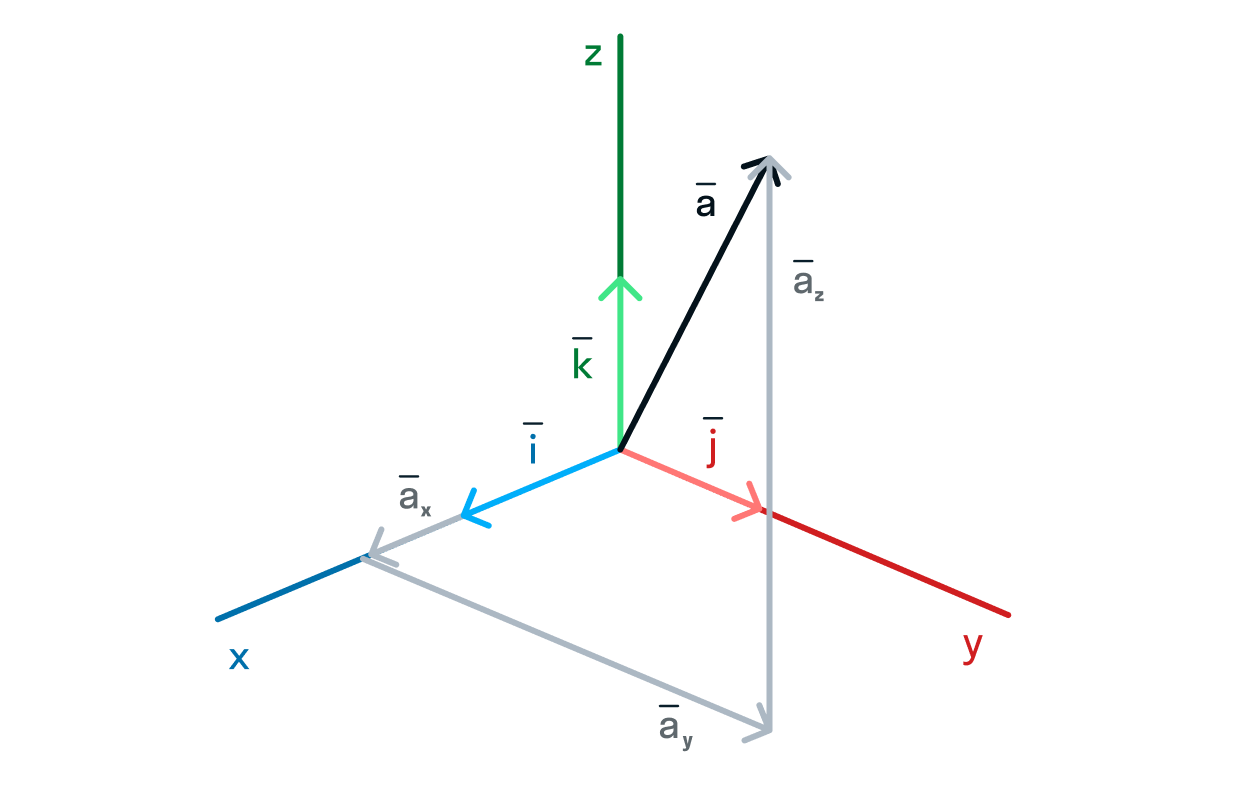
Любой вектор в трёхмерном пространстве можно разложить по трём базисным векторам.
с координатами можно записать так:
Умножение вектора на число
Представьте, что нам необходимо растянуть вектор в два раза или же сжать, но уже в три. За все эти действия отвечает одна простая задача: умножение вектора на число.
Для того чтобы увеличить или уменьшить вектор в некоторое количество раз, необходимо умножить все координаты вектора на это число.
Таким образом, если задан координатами то — Кстати, подобным образом можно перевернуть вектор, направив его в противоположную сторону:
Длина вектора
Длина вектора — одно из основных понятий в этом разделе. И неудивительно, ведь она характеризует его протяженность в пространстве и выражается числом.
Итак, длина вектора — это расстояние между его началом и концом. Её часто называют модулем, что отражается и в обозначении. Если нам необходимо найти длину мы так и запишем:
Длину вектора можно найти разными способами, вот основные:
- через координаты вектора;
- через координаты точек начала и конца вектора;
- через теорему косинусов.
Давайте вместе разберём все методы!
Длина вектора через его координаты
Если задан через координаты то его длину можно найти как
Почему мы можем быть уверены, что эта формула правильная? Рассмотрим вектор в декартовой системе координат.
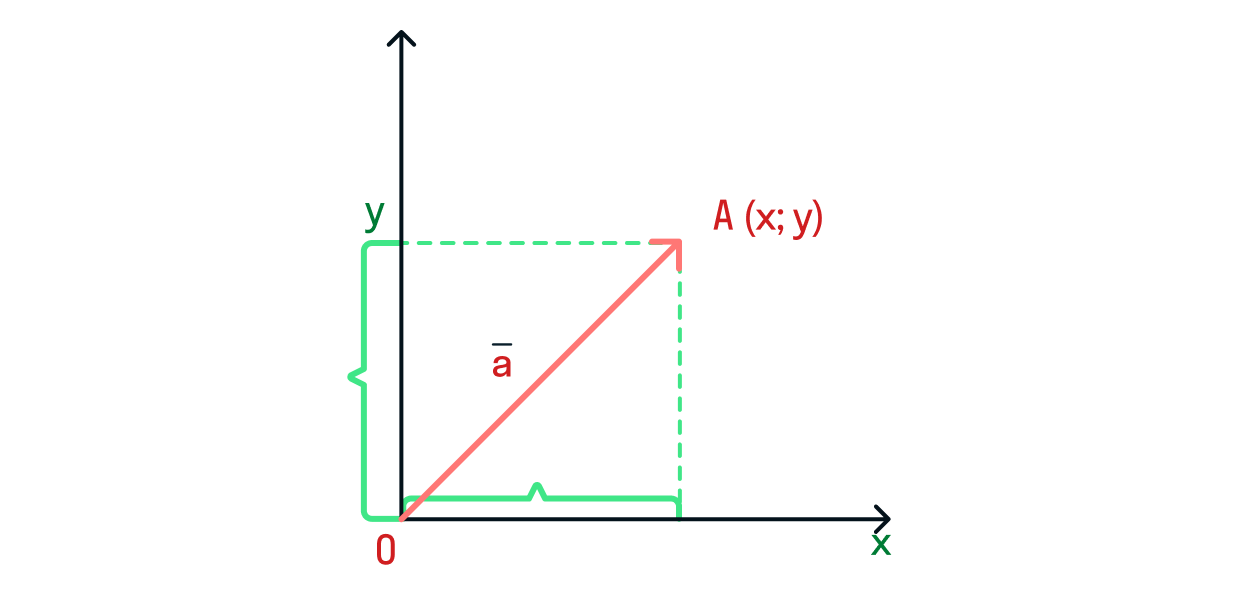
Отложим вектор от точки с координатами Тогда этот вектор можно назвать , и так как мы строили его из начала координат, координаты вектора могут быть найдены как
Рассчитаем длину через теорему Пифагора:
Задача 1
Посчитайте, чему равен модуль , если его координаты
Модуль вектора — это его длина, а значит,
Задача 2
Длина Чему равна координата по оси , если координата по оси
Длина вектора через координаты точек начала и конца
Для начала давайте вспомним, как задать координаты вектора через координаты его начала и конца.

Рассмотрим где и Тогда координаты вектора можно выразить так: