P — это число «π», математическая константа. Она соответствует соотношению между длиной окружности и длиной ее диаметра. Древнее название для π — число Лудольфо. Это число является иррациональным; его десятичное представление никогда не заканчивается после знака.
Определение периметра
Окружность — это сумма длин всех сторон многоугольника.
Какая буква обозначает окружность? Заглавная латинская буква P. Практично писать название фигуры в нижнем регистре под буквой P, чтобы не запутаться при решении задач.
В каких единицах измеряется окружность? Те же единицы измерения, что и для длины, например, миллиметры, сантиметры, метры, футы, дюймы, локти и т.д.
Если в задаче длины сторон даны в разных единицах длины, то окружность фигуры определить невозможно. Чтобы правильно решить эту задачу, нам необходимо перевести все данные в одну единицу измерения.
Узнайте, в чем заключаются ваши проблемы, и решите их без заучивания формул и скучных лекций.
Периметр прямоугольника. Как найти периметр прямоугольника?

Формулы нахождения периметра
Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. Поэтому, чтобы найти его, нам нужно знать длины этих сторон. Давайте рассмотрим, как найти периметр на примере некоторых фигур.
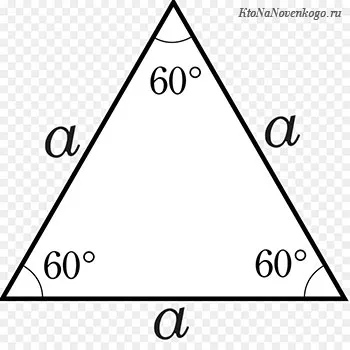
Равносторонний многоугольник
В равностороннем треугольнике все стороны имеют одинаковую длину. Таким образом, периметр равностороннего треугольника можно найти, умножив длину одной стороны на количество сторон, которое равно 3.
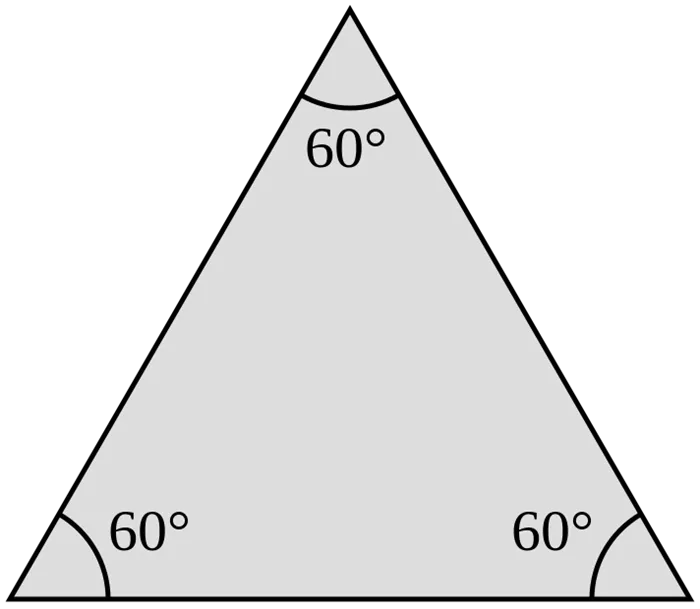
P = 3 ⋅ a, где a — длина стороны.
Периметр любого другого равностороннего многоугольника можно найти таким же образом: Умножьте длину сторон на их количество. Например, у квадрата и ромба все стороны одинаковой длины, поэтому их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.
Формула для равностороннего n-угольника: P = n ⋅ a, где a — длина стороны, а n — количество сторон.
Понятие четной и нечетной функции. Как определить четность и нечетность функции?
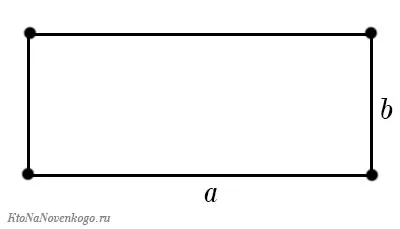
Прямоугольник и параллелограмм
Прямоугольник и параллелограмм имеют одинаковые стороны, поэтому легко определить их периметр, если известны две смежные стороны.
P = 2 ⋅ (a + b), где a — сторона, а b — смежная сторона.

Окружность
У круга нет окружности, потому что он не является многоугольником. Но у него есть длина, которую можно определить, зная радиус. Длина окружности равна произведению π на два радиуса или произведению π на диаметр.
L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, а π — константа, выражающая отношение окружности к диаметру и равная примерно 3,14.
Что такое периметр. Как найти периметр многоугольника?
Можно ли выучить все формулы, или, запомнив определение суммы всех сторон, можно быть умным и каждый раз вычислять ее самостоятельно. Давайте поупражняемся в определении периметра фигур!
Решение задач
Площадь прямоугольника равна 80 см2, а его длина — 10 см. Каков периметр фигуры?
- Для использования формулы P = 2 × (a + b), нам нужно найти ширину;
- Так как S = a × b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
- Далее подставляем известные данные в формулу: (10 + 8) × 2 = 36 см;
Периметр равнобедренного треугольника равен 40 см, а периметр
- Мы знаем, что периметр — это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания — получим сумму двух оставшихся сторон: 40 − 6 = 34 см;
- Известно, что равнобедренный треугольник имеет две равные стороны;
- Далее делим получившуюся сумму на два: 34 : 2 = 17 см;
Вычислить периметр многоугольников очень просто. Вам нужно только сложить длины всех сторон. Неважно, насколько сложными выглядят сами формы.
Давайте рассмотрим периметры наиболее распространенных фигур.
- Периметр равностороннего пятиугольника равен 4 × 5 = 20 см, значит, радиус окружности равен 20 см;
- Длина окружности равна π × 2 × 20 = 40π см;
Умножение двузначных, трехзначных и многозначных чисел столбиком. Как умножать в столбик?
Как упоминалось ранее, периметр треугольника можно вычислить простым сложением всех сторон.
Что такое периметр
Периметр обозначается латинской буквой «P». Он будет равным:
Если треугольник является равносторонним или так называемым правильным треугольником, то формула значительно упрощается.
Правильный треугольник характеризуется тем, что его противоположные стороны равны.
Расчет периметра многоугольников
P = a + b + a + b = 2a + 2b = 2 (a + b)
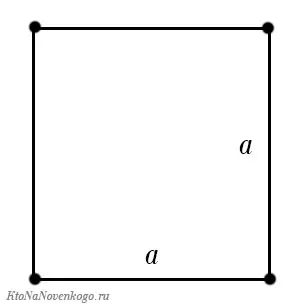
Как и в случае с треугольником, для прямоугольника существует особый случай, когда все стороны равны. И все знают, что такая форма называется квадратом.
Периметр треугольника
P = a + a + a + a + a = 4a.
На случай, если кто-то забыл: Прямоугольник — это квадрат, противоположные стороны которого равны и параллельны друг другу.
Его периметр такой же, как у прямоугольника. Кроме того, прямоугольник является частным случаем параллелограмма.
Периметр прямоугольника
P = a + a + a + b = 2a + 2b = 2 (a + b)
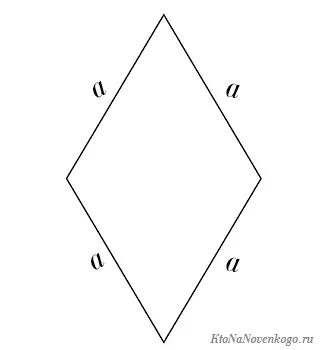
Существует еще один особый случай для параллелограмма. Он называется ромбом. Он называется ромбом.
Его периметр рассчитывается так же, как и периметр квадрата.
P = a + a + a + a + a = 4a.
Периметр параллелограмма
Есть еще одна фигура, которая часто встречается в жизни. И этому посвящены отдельные главы школьной программы. Трапеция — это четырехугольник, у которого только две стороны лежат на параллельных прямых.
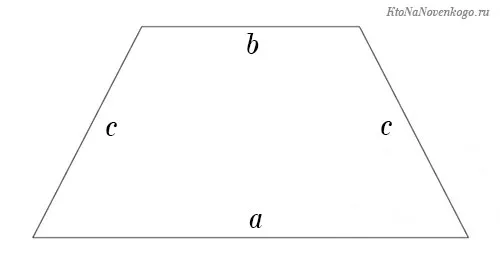
Однако существует особый случай, называемый равнобедренной трапецией. Эта фигура имеет непараллельные стороны, которые равны друг другу и имеют одинаковый наклон.

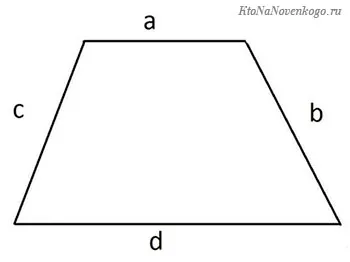
P = a + b + c + c = a + b + 2c
У нас есть своя формула для вычисления окружности круга, которая на самом деле является периметром фигуры. Только, в отличие от полигонов, эта величина обозначается латинской буквой «L».
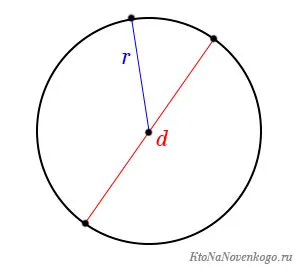
В этой формуле r означает радиус круга, т.е. расстояние от его центра до края. А буква π — это математическая константа, равная 3,14 (хотя в действительности количество знаков после запятой бесконечно).
P = a + a + a + a + a = 4a.
Периметр трапеции
Найдите периметр параллелограмма, если его смежные стороны равны $a$ и $b$.
Смежные и вертикальные углы. Что такое смежные углы?
Так как противоположные стороны равны по величине, то получается
Вывод: Чтобы найти периметр параллелограмма, умножьте сумму длин соседних сторон на 3500.
Расчет длины окружности
Трапеция — это геометрическая фигура, которая имеет четыре стороны, причем две противоположные стороны, называемые основаниями, параллельны друг другу (рис. 4).
Найдите периметр трапеции, если se
Источник: dorogaznaniy.ru
Что такое периметр? Как найти периметр? Периметр квадрата и прямоугольника. Способы определения и примеры решения Как посчитать периметр фигуры
Сегодня у нас речь пойдет о том, как вычислить периметр многоугольника . Но сначала поговорим о многообразии фигур. Посмотрите на рисунок. Какие фигуры мы здесь видим? Это прямоугольник и квадрат – многоугольники, которые имеют по четыре стороны, а также треугольник, имеющий три стороны, и пятиугольник с пятью сторонами.
И как же найти периметр этих фигур?
Для того, чтобы найти периметр многоугольника надо сложить длины всех его сторон .
Периметр обозначается заглавной латинской буквой Р .
Давайте рассмотрим несколько примеров.

Вычислим периметр многоугольника О. Как мы говорили ранее, периметр многоугольника – это сумма длин всех его сторон. Сложим все стороны нашего многоугольника:
Р = 15 + 17 + 10 + 10 + 20 + 15 = 87
Но можно вычислить периметр и другим способом, используя умножение. Мы видим, что некоторые стороны многоугольника одинаковы. У нас две стороны по 15 условных единиц и еще две по 10. Запишем выражение:
Р = 15 × 2 + 10 × 2 + 17 + 20 = 87
Теперь поговорим об особенностях вычисления периметра некоторых многоугольников.

Прямоугольник – это такой четырехугольник, у которого противоположные стороны равны. Например, чтобы вычислить А со сторонами а и б , надо сложить эти стороны и умножить полученный результат на 2 :
Р(прямоугольника) = (а + б) × 2
То есть, если сторона прямоугольника а = 5 см , а сторона прямоугольника б = 3 см , то периметр прямоугольника будет:
Р = (5 + 3) × 2 = 16 см
А как найти неизвестные стороны прямоугольника, если известен его периметр и только одна из сторон?
Р(прямоугольника) = 2 × а + 2 × б
а = (Р – 2 × б) ÷ 2 или б = (Р – 2 × а) ÷ 2
Пример: Периметр прямоугольника 16 см, сторона а = 5 см. Чему равны остальные стороны прямоугольника?
Если мы знаем одну сторону прямоугольника, значит длины двух, из четырех сторон нам известны. Найдем остальные две стороны. То есть найдем одну, а вторая будет ей равна.
сторона б = (16 – 2 × 5) ÷ 2 = 3 см
Ответ: у прямоугольника две стороны по 5 см и две по 3 см.

Квадрат – это прямоугольник, у которого все стороны равны. Чтобы вычислить надо длину одной стороны умножить на 4:
Р(квадрата) = а × 4
Например, у квадрата В сторона а = 5 см. Чтобы найти его периметр:
Р(В) = 5 × 4 = 20 см
А если известен периметр квадрата, как найти длины его сторон? Очень просто, надо его периметр разделить на четыре:
Пример: Периметр квадрата 24 см. Чему равны его стороны?
Ответ: Стороны квадрата равны 6 см.

По подобию вычисления периметра квадрата вычисляется периметр всех равносторонних многоугольников . То есть равен длине одной его стороны умноженной на количество сторон.
Если длина одной стороны многоугольника равна а , а число его сторон равно n , то его периметр будет равен:
Р(равностороннего многоугольника) = а × n
Например, у пятиугольника Д сторона а = 6 см . Найдем его периметр:
Р(Д) = 6 × 5 = 30 см
Ну а если известен периметр равностороннего многоугольника, то вычислить длины его сторон очень просто, надо разделить его периметр на количество сторон.
Периметр — это сумма длин всех сторон многоугольника.
- Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
- Периметр измеряется в единицах длины: мм, см, м, км и т.д.
Отличительные особенности прямоугольника
- Прямоугольник – это четырехугольник.
- Все параллельные стороны равны
- Все углы = 90º.
- Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.
Как вычислить периметр прямоугольника
Существует 2 способа его нахождения:
- 1 способ. Складываем все стороны. P = a + а + b + b
- 2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
«a» — длина прямоугольника, более длинная пара его сторон.
«b» — ширина прямоугольника, более короткая пара его сторон.
Пример задачи на подсчет периметра прямоугольника:
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.

Запомни формулы вычисления периметра прямоугольника!

Полупериметр — это сумма одной длины и одной ширины.
- Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
- Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.
Как найти площадь прямоугольника
Формула площади прямоугольника S= a*b
Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.
- : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.

- Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
- Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)
Цель: ознакомить с приёмом нахождения периметра прямоугольника.
Задачи: формировать умение решать задачи, связанные с нахождением периметра фигур, вырабатывать умения чертить геометрические фигуры, закрепить умение вычислять, применяя с переместительное свойство сложения, развивать навык устного счёта, логическое мышление, воспитывать познавательную активность и умение работать в коллективе.
Оборудование: ИКТ (мультимедийный проектор, презентация к уроку), картинки с геометрическими фигурами для физминутки, модель магического квадрата, у учеников – модели геометрических фигур, маркерные доски, линейки, учебники, тетради.
1. Организационный момент
Проверка готовности к уроку. Приветствие.
Начинается урок,
Он пойдёт ребятам впрок.
Постарайтесь всё понять –
И внимательно считать.
2. Устный счёт
а) Использование магических фигур. (Приложение 1 )
– Заполним клетки магического квадрата, назовите его особенности (сумма чисел по горизонталям, вертикалям и диагоналям равны) и определите волшебное число. (39)
По цепочке дети заполняют квадрат на доске и в тетрадях .
б) Знакомство со свойствами магических треугольников. (Приложение 2 )
– Суммы чисел в углах, образующие треугольник равны. Найдём волшебные числа у треугольника. Определи пропущенное число. Отметь его на маркерной доске.
3. Подготовка к изучению нового материала
– Перед Вами геометрические фигуры. Назовите их одним словом. (Четырёхугольники).
– Разделите их на 2 группы. (Приложение 3 )
– Что такое прямоугольники. (Прямоугольники – четырехугольники, у которых все углы прямые.)
– Что можно узнать, зная длины сторон четырёхугольников? Периметр – сумма длин сторон фигур.
– Найдите периметр белой фигуры, жёлтой.
– Почему у прямоугольников известны не все стороны?
– Какие свойства у противолежащих сторон прямоугольников? (У прямоугольника противоположные стороны равны).
– Если противоположные стороны равны, надо ли измерять все стороны? (Нет.)
– Правильно, достаточно измерить длину и ширину.
– Как вычислить удобным способом? (Учащиеся работают устно с комментированием.)
4. Изучение новой темы
– Прочитайте тему нашего урока: «Периметр прямоугольника». (Приложение 4 )
– Помогите найти периметр данной фигуры, если её длина равна – а , а ширина – в .
Желающие находят Р у доски. Учащиеся в тетрадях записывают решение.
– Как записать это по-другому?
Р = а + а + в + в ,
Р = а х 2 + в х 2,
Р = (а + в ) х 2.
– Мы получили формулу нахождения периметра прямоугольника. (Приложение 5 )
5. Закрепление
Дети читают и записывают условие, вопрос, чертят фигуру, находят Р разными способами, записывают ответ.
6. Физминутка. Сигнальные карточки
Сколько клеточек зелёных,
Столько выполним наклонов.
Столько раз руками хлопнем.
Столько раз ногами топнем.
Сколько здесь у нас кружков,
Столько сделаем прыжков.
Мы присядем столько раз,
Столь подтянемся сейчас.
7. Практическая работа
– У Вас на партах лежат в конвертах геометрические фигуры. Как мы их назовём?
– Что такое прямоугольники?
– Что вы знаете о противолежащих сторонах прямоугольников?
– Измерьте стороны фигур по вариантам, найдите периметр разными способами.
– Проверяем у соседа.
Взаимопроверка тетрадей .
– Прочитайте: Как нашли периметр? Что можно сказать о периметрах данных фигур? (Они равны) .
– Начертите прямоугольник с таким же Р, но другими сторонами.
Р 1 = (2 + 6) х 2 = 16 Р 1 = 2 х 2 + 6 х 2 = 16
Р 1 = 2 + 2 + 6 + 6 = 16
Р 2 = 3 + 3 + 5 + 5 = 16 Р 2 = (3 + 5) х 2 = 16
Р 3 = 4 + 4 + 4 + 4 = 16 Р 4 = 1 + 1 + 7 + 7 = 16
8. Графический диктант
Слева 6 клеток. Поставили точку. Начинаем движение. 2 – вправо, 4 – вправо вниз, 10 – влево, 4 – вправо вверх. Какая фигура?
Преврати её в прямоугольник. Дострой. Найди Р разными способами.
Р = (5 + 2) х 2 = 14.
Р = 5 + 5 + 2 + 2 = 14.
Р = 5 х 2 + 2 х 2 = 14.
9. Пальчиковая гимнастика
Умножали, умножали.
Очень, очень мы устали.
Наши пальчики сплетём и соединим ладошки.
А потом, как только можем, крепко накрепко сожмём.
На дверях висит замок.
Кто его открыть не смог?
Мы замочком постучали,
Мы замочек повертели,
Мы замочек покрутили и открыли.
(Слова сопровождаются движениями)
10. Составление и решение задачи по условию (Приложение 8 )
Длина прямоугольника – 12 дм
Ширина – на 3 дм м.
Р – ?
В первом действии найдём ширину: 12 – 3 = 9 (дм) – ширина
Зная длину и ширину, узнаем Р одним из способов.
Р = (12 + 9) х 2 = 42 дм
11. Самостоятельная работа
12. Итог урока
– Чему учились. Как находили Р прямоугольника?
13.Оценивание
Оцениваются ответы учащихся у доски и выборочно в процессе самостоятельной работы.
14.Домашнее задание
С. 44 № 5 (с пояснениями).
Умение находить периметр прямоугольника очень важно для решения многих геометрических задач. Ниже приведена подробная инструкция по нахождению периметра разных прямоугольников.
Как найти периметр обычного прямоугольника
Обычный прямоугольник – четырехугольник, у которого параллельные стороны равны и все углы = 90º. Для нахождения его периметра существует 2 способа:
Складываем все стороны.
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина – 6.
Решение (последовательность действий и рассуждения):
- Так как нам известны ширина и длина прямоугольника, найти его периметр не составит труда. Ширина параллельна ширине, а длина длине. Таким образом, в обычном прямоугольнике 2 ширины и 2 длины.
- Складываем все стороны (3 + 3 + 6 + 6) = 18 см.
Второй способ заключается в следующем:
Нужно сложить ширину и длину, и умножить на 2. Формула этого способа имеет следующий вид: 2×(a + b), где a – ширина, b – длина.
В рамках данной задачи получим такое решение:
Как найти периметр прямоугольника – квадрат
Квадрат является правильным четырехугольником. Правильным потому, что все его стороны и углы равны. Для нахождения его периметра так же существует два способа:
- Сложить все его стороны.
- Умножить его сторону на 4.
Пример: Найти периметр квадрата, если его сторона = 5 см.
Так как нам известна сторона квадрата, мы сможем найти его периметр.
Складываем все стороны: 5 + 5 + 5 + 5 = 20.
Умножаем сторону квадрата на 4 (потому что все равны): 4×5 = 20.
Как найти периметр прямоугольника – онлайн-ресурсы
Несмотря на то, что вышеупомянутые действия легки для понимания и освоения, вам может пригодиться несколько онлайн-калькуляторов, которые помогут вам вычислить периметры (площадь, объем) разных фигур. Просто вбейте необходимые значения и мини-программа рассчитает периметр нужной вам фигуры. Ниже приведен небольшой список.
Урок и презентация на тему: «Периметр и площадь прямоугольника»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D .

Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.
Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
P ABCD = 2 * (AB + BС)
P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: P ABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.
P ABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
P ABCD = 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:
P ABCD = 4 * AB
3. Подставим в формулу наши данные:
P ABCD = 4 * 6 см = 24 см
Ответ: P ABCD = 24 см.
Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.

2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM

Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.

Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB

Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см 2
Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
Источник: rt82.ru
Периметр прямоугольника определение – Периметр прямоугольника. Видеоурок. Математика 2 Класс

Периметр прямоугольника. Видеоурок. Математика 2 Класс
На этом занятии мы познакомимся с новым понятием – периметр прямоугольника. Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.
На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.
Рассмотрим следующую геометрическую фигуру (рис. 1):
Рис. 1. Прямоугольник
Данная фигура – прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Прямоугольник – это четырехугольник, у которого четыре прямых угла и стороны попарно равны.
Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.
Рассмотрим следующую задачу:
Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка – 5 метров, длина – 10 метров. Забор какой длины получится у строителей?
Рис. 2. Иллюстрация к задаче 1
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10).
Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.
Ответ: 30 метров.
Периметр прямоугольника – сумма длин всех его сторон. Формула для подсчета периметра прямоугольника: , здесь a – длина прямоугольника, а b – ширина прямоугольника. Сумма длины и ширины называется
полупериметром. Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).
Периметр любой фигуры измеряется в линейных единицах.
На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.
Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.
Если периметр – это сумма длин всех сторон фигуры, то полупериметр – сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках – (a+b)).
Список литературы
- Александрова Э.И. Математика. 2 класс. – М.: Дрофа, 2004.
- Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. – М.: Астрель, 2006.
- Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. – М.: Просвещение, 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Festival.1september.ru (Источник).
- Nsportal.ru (Источник).
- Math-prosto.ru (Источник).
Домашнее задание
- Найти периметр прямоугольника, у которого длина 13 метров, а ширина – 7 метров.
- Найти полупериметр прямоугольника, если его длина – 8 см, а ширина – 4 см.
- Найти периметр прямоугольника, если его полупериметр – 21 дм.
Что такое периметр?
Периметр — один из математических, а точнее — геометрических терминов, применяется в основном для вычисления сторон фигуры.
Из нашей статьи вы узнаете, что такое периметр и как он измеряется на примере основных геометрических фигур.
Определение периметра
Периметром называют общую длину всех сторон или окружности той или иной фигуры. Обозначается периметр большой буквой «Р», а измерять его можно в различных единицах длины, таких как миллиметры (мм), сантиметры (см), метры (м) и т. д. Для различных фигур существуют различные формулы для нахождения периметра. Ниже мы приведем несколько примеров, как узнать периметр у прямоугольника и некоторых других фигур.
Измеряем периметр
Для того чтобы узнать периметр какого-либо многоугольника, вам понадобится линейка. Измерив все стороны многоугольника линейкой и сложив вместе полученные цифры, вы узнаете, каков его периметр. Например, у вас получились стороны 13, 14, 15 и 17 сантиметров, складываем и получаем P = 13 + 14 + 15 + 17 = 59 см. Более подробную информацию о нахождении периметра у различных многоугольников вы сможете узнать из нашей статьи Как найти периметр многоугольника.
Если вам необходимо узнать периметр у сложной фигуры (к таким фигурам можно отнести фигуры с неровными линиями), то для этого вам понадобится веревка или нитка. При помощи этих вещей необходимо описать точный контур фигуры, а чтобы не запутаться, вы можете на веревке сделать отметки карандашом. Или же можно просто ее обрезать, а после приложить все части к линейке. Таким образом, вы узнаете, чему равен периметр практически у любой сложной фигуры.
Существует еще одно приспособление для вычисления периметра у сложных фигур: его называют курвиметр (роликовый дальномер). С его помощью вам нужно установить ролик в любую точку фигуры и описать роликом контур фигуры. Полученное число и будет равно периметру. О нахождении периметра у других геометрических фигур вы сможете узнать из нашей статьи Как найти периметр. Ну а мы расскажем ещё о нескольких способах изменения периметра для разных фигур.
Круг, квадрат, равносторонний треугольник
Иногда для того, чтобы определить значение периметра у некоторых фигур, не нужно складывать все стороны, а достаточно воспользоваться умножением. Например, для нахождения периметра у равностороннего треугольника необходимо значение длины стороны умножить на 3. Например, если сторона — 12 см, то Р = 12 х 3 = 36 см, так как все стороны имеют одинаковую длину. Другую интересную информацию о треугольниках вы узнаете, прочитав нашу статью Что такое периметр треугольника.
Давайте также рассмотрим, как узнать периметр круга. Это довольно-таки просто: достаточно лишь определить длину окружности, а сделать это можно, умножив радиус «r» на число π≈3,14 и затем на 2 (P=L=2∙
диагонали равны и в точке пересечения делятся пополам;
сумма квадратов диагоналей равна сумме квадратов всех (четырех) сторон;
прямогугольниками одного размера можно полностью замостить плоскость;
прямоугольник можно двумя способами разделить на два равных между собой прямоугольника;
прямоугольник можно разделить на два равных между собой прямогульных треугольника;
вокруг прямоугольника можно описать окружность, диаметр которой равен диагонали прямоугольника;
в прямогульник (кроме квадрата) нельзя вписать окружность так, чтобы она касалась всех его сторон.
Параллельность сторон, одинаковость углов и возможность замощения плоскости делают прямоугольник самой удобной геометрической фигурой при разбиении площади на участки будь то на местности, в помещении или внутри технического устройства. Участок можно считать прямоугольным, если его отклонения от идеального прямоугольника не превышают допустимой в расчетах погрешности. Тогда для периметр и площадь участка можно определять по формулам расчета периметра и площади прямоугольника.
Периметр P прямоугольника равен удвоенной сумме сторон, прилежащих к одному углу
Длина диагонали d прямоугольника вычисляется по теореме Пифагора:
Углы между диагоналями прямоугльника определяются соотношением сторон:
α = 2arctg(a/b),
β = 2arctg(b/a),
α + β = 180°.
Площадь S прямоугольника равна произведению сторон, прилежащих к одному углу (произведению длины на ширину):
Также можно выразить площадь прямоугольника через длину диагоналей и угол между ними:
Радиус описанной вокруг прямоугольника окружности равен половине длины диагонали:
В прямоугольник (если он не квадрат) нельзя вписать окружность так, чтобы она касалась всех его сторон. Максимальный радиус окружности, которая может поместиться внутри прямоугольника, равен половине его меньшей стороны.
Формулы периметра.
Периметром геометрической фигуры — называют длину границы геометрической фигуры.
Формула периметра треугольника

Периметр треугольника ∆ABC равен сумме длин его сторон
Формулы периметра квадрата

Периметр квадрата равен произведению длины его стороны на четыре.
Периметр квадрата равен произведению длины его диагонали на два корня из двух.
где P — периметр квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула периметра прямоугольника

Периметр прямоугольника ABCD равен удвоенной сумме сторон, прилежащих к одному углу.
где P — периметр прямоугольника,
— длины сторон прямоугольника.
Формула периметра параллелограмма
Периметр параллелограмма ABCD равен удвоенной сумме сторон, прилежащих к одному углу
где P — периметр параллелограмма,
— длины сторон параллелограмма.
Формула периметра ромба
Периметр ромба равен произведению длины его стороны на четыре.
где P — периметр ромба,
— длина стороны ромба.
Формула периметра трапеции

Периметр трапеции равен сумме длин ее сторон.
где P — периметр трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции.
Формулы периметра круга, длины окружности.

где P — периметр круга,
Как найти периметр прямоугольника? — Kak1000.ru

Прямоугольник обладает многими отличительными особенностями, исходя из которых, выработаны правила вычисления его различных числовых характеристик. Итак, прямоугольник:
Плоская геометрическая фигура;
Четырехугольник;
Фигура, у которой противоположные стороны равны и параллельны, все углы прямые.
Периметр – это общая длина всех сторон фигуры.
Вычисление периметра прямоугольника — довольно простая задача.
Все, что вам нужно знать, это ширину и длину прямоугольника. Поскольку прямоугольник имеет две равные длины и две равные ширины, измеряется только одна сторона.
Периметр прямоугольника равен удвоенной сумме 2-х его сторон длины и ширины.
P = (a + b) • 2, где a — длина прямоугольника, b — ширина прямоугольника.
Так же периметр прямоугольника можно найти при помощи суммы всех сторон.
P= a+a+b+b, где а– длина прямоугольника, b – ширина прямоугольника.
Периметр квадрата — это длина стороны квадрата, умноженная на 4.
P = a • 4, где a — длина стороны квадрата.
Дополнение: Нахождение найти площади и периметра прямоугольников
[smartcontrol_youtube_shortcode key=»площадь и периметр прямоугольника» cnt=»2″ col=»2″ shls=»false»]
В программе обучения за 3 класс предусмотрено изучение многоугольников и их особенностей. Для того чтобы понять, как найти периметр прямоугольника и площадь, разберемся, что подразумевается под этими понятиями.
Основные понятия
Нахождение периметра и площади требует знания некоторых терминов. К ним относятся:
- Прямой угол. Образуется из 2 лучей, имеющих общее начало в виде точки. При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника.
- Прямоугольник. Это четырехугольник, все углы которого являются прямыми. Его стороны называют длиной и шириной. Как известно, противоположные стороны этой фигуры равны.
- Квадрат. Является четырехугольником, все стороны которого равны.
При знакомстве с многоугольниками их вершины могут называться АВСД. В математике принято именовать точки на чертежах буквами латинского алфавита. В названии многоугольника перечисляют все вершины без пропусков, например, треугольник ABC.
Вычисление периметра
Периметр многоугольника — это сумма длин всех его сторон. Эта величина обозначается латинской буквой P. Уровень знаний для предложенных примеров — 3 класс.
Задача №1: «Начертите прямоугольник 3 см шириной и 4 см длиной с вершинами ABCD. Найдите периметр прямоугольника ABCD».
Формула будет выглядеть так: P=AB+BC+CD+AD либо P=AB×2+BC×2.
Ответ: P=3+4+3+4=14 (см) либо P=3×2 + 4×2=14 (см).
Задача №2: «Как найти периметр прямоугольного треугольника ABC, если значения сторон равны 5, 4 и 3 см?».
Ответ: P=5+4+3=12 (см).
Задача №3: «Найдите периметр прямоугольника, одна сторона которого равна 7 см, а другая на 2 см длиннее».
Чтобы найти периметр, сначала нужно высчитать неизвестное: 7+2=9.
Ответ: P=7+9+7+9=32 (см).
Задача №4: «Соревнования по плаванию проходили в бассейне, периметр которого составляет 120 м. Сколько метров проплыл участник соревнований, если ширина бассейна 10 м?».
В данной задаче стоит вопрос, как найти длину бассейна. Для решения найдите длины сторон прямоугольника. Ширина известна. Сумма длин двух неизвестных сторон должна составить 100 м. 120-10×2=100. Чтобы узнать расстояние, которое преодолел пловец, нужно разделить полученный результат на 2. 100_2=50.
Вычисление площади
Более сложной величиной является площадь фигуры. Для ее измерения используют мерки. Эталоном среди мерок являются квадраты.
Площадь квадрата со стороной 1 см равна 1 см². Квадратный дециметр обозначен как дм², а квадратный метр — м².
Области применения единиц измерения могут быть такими:
- В см² измеряют маленькие предметы, например фотографии, обложки учебников, листы бумаги.
- В дм² можно измерить географическую карту, оконное стекло, картину.
- Для измерения пола, квартиры, земельного участка используют м².
Если начертить прямоугольник 3 см длиной и 1 см шириной и разбить на квадраты со стороной 1 см, то в нем поместится 3 квадрата, а значит, его площадь составит 3 см². Если прямоугольник разбит на квадраты, найдем периметр прямоугольника также без затруднений. В данном случае он равен 8 см.
Другой способ посчитать количество квадратов, вмещающихся в фигуру, — это использование палетки. Начертим на кальке квадрат площадью 1 дм², что составляет 100 см². Поместим кальку на фигуру и посчитаем число квадратных сантиметров в одном ряду. После этого выясним количество рядов, а затем перемножим значения. Значит, площадь прямоугольника — это произведение его длины и ширины.
Способы сравнения площадей:
- На глаз. Иногда достаточно просто взглянуть на предметы, поскольку в некоторых случаях и невооруженным глазом видно, что одна фигура занимает больше места, как, например, учебник, лежащий на столе рядом с пеналом.
- Наложение. Если фигуры совпадают при наложении, их площади равны. Если же одна из них полностью помещается внутри второй, то ее площадь меньше. Места, занимаемые тетрадным листом и страницей из учебника, можно сравнить, наложив их друг на друга.
- По количеству мерок. Фигуры при наложении могут и не совпадать, однако иметь одинаковую площадь. Сравнить в этом случае можно, подсчитав количество квадратов, на которые разбита фигура.
- Числа. Сравниваются численные значения, измеренные одной и той же меркой, например, в м².
Далее предложены задачи на тему, как найти площадь и периметр прямоугольника, если известна другая величина.
Пример №1: «Швея сшила детское одеяло из квадратных разноцветных лоскутков. Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».
Чтобы решить задачу, нужно ответить на вопрос, как найти длину прямоугольника. Далее найдем периметр прямоугольника, составленного из квадратов. Из задачи ясно, что ширина одеяла — 5 дм, вычисляем длину, разделив 50 на 5, и получаем 10 дм. Теперь найдите периметр прямоугольника со сторонами 5 и 10. P=5+5+10+10=30.
[smartcontrol_youtube_shortcode key=»периметр прямоугольника» cnt=»2″ col=»2″ shls=»false»]
Пример №2: «На раскопках обнаружен участок, где могут находиться древние сокровища. Сколько территории придется исследовать ученым, если известен периметр 18 м и ширина прямоугольника 3 м?».
Определим длину участка, проделав 2 действия. 18-3×2=12. 12_2=6. Искомая территория будет также равна 18 м² (6×3=18).
Таким образом, зная формулы, вычислить площадь и периметр не составит труда, а приведенные выше примеры помогут попрактиковаться в решении математических задач.
Как узнать периметр (P) прямоугольника?
посчитать сумму всех сторон
(a+b)*2 например если сторона а = 5 см, а сторона b = 3 см то будет (5+3)*2=16см
Периметр прямоугольника равен удвоенной сумме 2-х его сторон или : P=2*(a+b)
Периметр это сумма длин всех сторон фигуры. Чтобы найти периметр прямоугольника, нужно сложить длины всех его сторон или сложить его длину и ширину и то, что получится умножить на 2. Например: Длина 10 см Ширина 5 см 1 способ: 10+10+5+5=30 см 2 способ: (10+5) *2=30 см Ответ: 30 см. С квадратом всё тоже самое, но есть ещё один способ. Нужно одну его сторону умножить на 4, так как у квадрата все стороны равны.
Источник: xn—-8sbanwvcjzh9e.xn--p1ai